微分を利用する体積などの変化率に関する例題です。
(例題1)
体積が毎分\(1m^3\)の割合で増大する球形の気球がある。その直径が\(5m\)となった瞬間における表面積の増大する速さを求めよ。
\(\displaystyle\frac{dS}{dt}=\displaystyle\frac{d}{dr}(4πr^2)\cdot\displaystyle\frac{dr}{dt}=8πr\cdot\displaystyle\frac{dr}{dt}\)
です。\(r=5\) を代入すればいいので、あとは \(\displaystyle\frac{dr}{dt}\) が判明すればおしまいですが、これは毎分\(1m^3\)の割合で増大するという条件から求めることができます。(体積を\(V\)を\(r\)で表し、同様に\(t\)で微分します)
(解答)
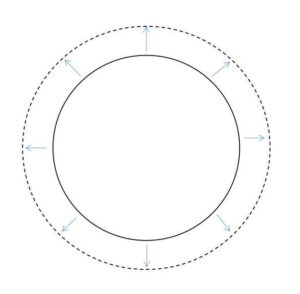
時刻\(t\)(分)のときの気球の半径を\(r(m)\)とすると、そのときの体積\(V\)は
\(V=\displaystyle\frac{4}{3}πr^3\)・・・①
体積が毎分\(1m^3\)の割合で増大するから、\(\displaystyle\frac{dV}{dt}=1\)
①の両辺を\(t\)で微分して
\(\displaystyle\frac{dV}{dt}=\displaystyle\frac{d}{dr}(\displaystyle\frac{4}{3}πr^3)\cdot\displaystyle\frac{dr}{dt}\)
よって
\(1=4πr^2\cdot\displaystyle\frac{dr}{dt}\)
\(\displaystyle\frac{dr}{dt}=\displaystyle\frac{1}{4πr^2}\)
また、半径\(r\)のときの表面積\(S\)は
\(S=4πr^2\)
両辺\(t\)で微分して
\(\displaystyle\frac{dS}{dt}=\displaystyle\frac{d}{dr}(4πr^2)\cdot\displaystyle\frac{dr}{dt}\)
ゆえに
\(\displaystyle\frac{dS}{dt}=8πr\cdot\displaystyle\frac{1}{4πr^2}\)
\(\displaystyle\frac{dS}{dt}=\displaystyle\frac{2}{r}\)
したがって直径が\(5m\) (半径\(\displaystyle\frac{5}{2}m\)) となった瞬間における表面積の増大する速さは
\(\displaystyle\frac{dS}{dt}=\displaystyle\frac{2}{\displaystyle\frac{5}{2}}\)\(=\displaystyle\frac{4}{5}(m^2/分)\)
(例題2)
図のような底なしの正四角錐を逆さまにした容器がある。高さ\(4cm\)のところで水平断面は\(1\)辺\(3cm\)の正方形である。この容器に\(9cm^3/s\)で静かに水を入れるとき、水の深さが\(2cm\)になる瞬間の水面が上昇する速さは何\(cm/s\)か。
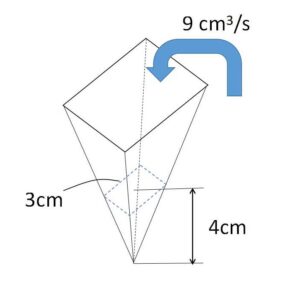
\(V=\displaystyle\frac{1}{3}a^2h\)
で、\(a\)と\(h\)の比の関係は\(3:4\)なので、\(a\)が消去できます。あとは\(t\)で微分するだけです。
(解答)
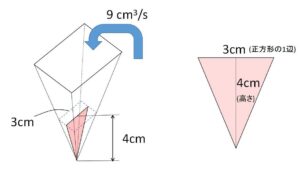
時刻\(t(s)\)での水の深さ(水でできる四角錐の高さ)を\(h(cm)\)、水面の正方形の1辺の長さを\(a(cm)\)、体積を\(V(cm^3)\)とする。
\(V=\displaystyle\frac{1}{3}a^2h\)・・・①
また、\(a:h=3:4\) だから
\(a=\displaystyle\frac{3}{4}h\)
これを①に代入して
\(V=\displaystyle\frac{1}{3}(\displaystyle\frac{3}{4}h)^2h\)
\(V=\displaystyle\frac{3}{16}h^3\)・・・③
③の両辺を\(t\)で微分して
\(\displaystyle\frac{dV}{dt}=\displaystyle\frac{d}{dh}(\displaystyle\frac{3}{16}h^3)\cdot\displaystyle\frac{dh}{dt}\)
\(9cm^3/s\)で水を入れるので
\(\displaystyle\frac{dV}{dt}=9\)
よって
\(9=\displaystyle\frac{9}{16}h^2\cdot\displaystyle\frac{dh}{dt}\)
\(\displaystyle\frac{dh}{dt}=\displaystyle\frac{16}{h^2}\)・・・④
したがって水の深さが\(2cm\)になる瞬間の水面が上昇する速さは、④に\(h=2\)を代入して
\(\displaystyle\frac{dh}{dt}=4(cm/s)\)
(例題2)だと、時刻\(t\)で変化するのは「水面の高さ、水面の正方形の1辺の長さ(それに伴う正方形の面積)、水の体積」などで、変化しないのは「体積の増加速度」(体積自体は増加する)です。そして求めたいのは \(h=2\) における \(\displaystyle\frac{dh}{dt}\) です。微分する変数は時刻\(t\)であるのはよいでしょう。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→1次近似式 back→グラフ上の点の速度・加速度