1次式への近似について見ていきます。
しかし、現実世界ではもちろん精密な数値が要求される場合もあるとは思いますが、大まかな値でよいことが多いのもまた事実です。
・1次近似式
微分の定義より、1次式の近似式を導くことができます。
\(\displaystyle\lim_{h \to 0}\displaystyle\frac{f(a+h)-f(a)}{h}=f'(a)\)
より、\(h\)が\(0\)に近いとき
\(\displaystyle\frac{f(a+h)-f(a)}{h}≒f'(a)\)
と近似できます。よって \(f(a+h)\) を次のように\(h\)の1次式で表すことができます。
\(f(a+h)≒f(a)+f'(a)h\)・・・①
また微分の定義の別の表し方
\(\displaystyle\lim_{x \to a}\displaystyle\frac{f(x)-f(a)}{x-a}=f'(a)\)
より、\(x\)が\(a\)に近いとき \(f(x)\) を次のように\(x\)の1次式で表すことができます。
\(f(x)≒f(a)+f'(a)(x-a)\)・・・②
同じ微分の定義から出発したので、①と②は本質的には同じ式です。実際①で \(h=x-a\) と変換すると②になります。これらは \(x=a\) 付近 (\(x=a\) まわり) での\(f(x)\)の近似式ですが、①が特にそれを強調した形になっています。
また、②の右辺は\(f(x)\)の \(x=a\) における接線の方程式なので、②は(①も) \(f(x)\) を接線(1次式)で近似していることになります。図の赤線部が実際の関数とのズレ(誤差)です。
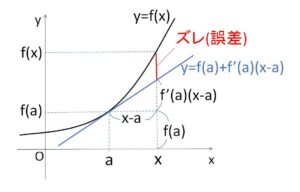
そしてとくに \(x=0\) 付近での1次近似式は、①で\(h=x\)、\(a=0\) とするか、②で\(a=0\) とするかで次のように得ることができます。
\(x\)が\(0\)に近いとき
\(f(x)≒f(0)+f'(0)x\)
①\(h\)が\(0\)に近いとき
\(f(a+h)≒f(a)+f'(a)h\)
②\(x\)が\(a\)に近いとき
\(f(x)≒f(a)+f'(a)(x-a)\)
とくに \(x=0\) 付近 (\(a=0\)) だと
\(f(x)≒f(0)+f'(0)x\)
変化量に着目した微分の式
\(\displaystyle\lim_{Δx \to 0}\displaystyle\frac{Δy}{Δx}=y’\)
から導かれる近似式もありますが、これは次回に扱いたいと思います。これも合わせると全部で3つの1次近似式になりますが、本質的にはどれも同じです。
(例題1)
(1)\(f(x)=\sqrt{x+1}\) について、\(|x|\)が十分小さいとき \(f(x)\) の1次近似式を作れ。
(2) (1)の近似式を\(g(x)\) とおくとき、次の不等式が成り立つことを示せ。
\(0<g(x)-f(x)<\displaystyle\frac{1}{8}x^2\) (ただし、\(x>0\))
(3)近似式\(g(x)\)を利用して、\(\sqrt{17}\) を小数第1位まで求めよ。
(解答)
(1)
ただし①だと \(F(h+1)≒F(1)+F'(1)h\) になるので、\(F(x)=\sqrt{x}\) とする必要があるので、後者を使った方が楽です。
\(|x|\)が十分小さいとき
\(f(x)≒f(0)+f'(0)x\)
\(f(x)=\sqrt{x+1}\) より
\(f'(x)=\displaystyle\frac{1}{2\sqrt{x+1}}\)
だから
\(f(0)=1\)、\(f'(0)=\displaystyle\frac{1}{2}\)
よって
\(f(x)≒1+\displaystyle\frac{1}{2}x\)
(2)
微分してもよいですが、有理化して示すと楽です。
(1)より
\(g(x)=1+\displaystyle\frac{1}{2}x\)
だから
\(g(x)-f(x)=1+\displaystyle\frac{1}{2}x-\sqrt{x+1}\)
\(=\displaystyle\frac{(1+\displaystyle\frac{1}{2}x)^2-(x+1)}{(1+\displaystyle\frac{1}{2}x)+\sqrt{x+1}}\)
\(=\displaystyle\frac{x^2}{(4+2x)+4\sqrt{x+1}}\)
よって \(x>0\) より
\(0<g(x)-f(x)<\displaystyle\frac{x^2}{(4+0)+4\sqrt{0+1}}\)
\(0<g(x)-f(x)<\displaystyle\frac{x^2}{8}\)
(3)
\(\sqrt{17}=4\sqrt{\displaystyle\frac{17}{16}}=4\sqrt{1+\displaystyle\frac{1}{16}}\)
\(|\displaystyle\frac{1}{16}|\)は小さいので、(1)より
\(f(\displaystyle\frac{1}{16})=\sqrt{1+\displaystyle\frac{1}{16}}≒1+\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{16}=\displaystyle\frac{33}{32}\)
よって
\(\sqrt{17}≒4×\displaystyle\frac{33}{32}=\displaystyle\frac{33}{8}\)
\(≒4.1\)
(参考)
(2)より
\(0<(1+\displaystyle\frac{1}{2}x)-\sqrt{x+1}<\displaystyle\frac{1}{8}x^2\)
なので、辺々\(4\)倍して
\(0<(4+2x)-\sqrt{16(x+1)}<\displaystyle\frac{1}{2}x^2\)
\(x=\displaystyle\frac{1}{16}\) を代入すると
\(0<\displaystyle\frac{33}{8}-\sqrt{17}<\displaystyle\frac{1}{2}(\displaystyle\frac{1}{16})^2\)
よって
\(0<(近似値)-\sqrt{17}<\displaystyle\frac{1}{512}\)
となるので、近似値 \(\displaystyle\frac{33}{8}\) と \(\sqrt{17}\) の誤差は \(\displaystyle\frac{1}{512}\) (約\(0.002\)) より小さいことになります。
(例題2)
\(\sin29°\) の近似値を1次近似式を利用して小数第3位まで示せ。ただし \(π=3.14\)、\(\sqrt{3}=1.73\) とせよ。
いずれにせよ、微分を利用するので弧度法で考える必要があります。
(解答1)
\(\sin(29°)=\sin(30°-1°)=\sin(\displaystyle\frac{π}{6}-\displaystyle\frac{π}{180})\)
\(f(a+h)≒f(a)+f'(a)h\) (\(h\)は\(0\)に近い)
において、\(f(x)=\sin x\) 、\(a=\displaystyle\frac{π}{6}\)、\(h=-\displaystyle\frac{π}{180}\) とすると、\(f'(x)=\cos x\) より
\(\sin(\displaystyle\frac{π}{6}-\displaystyle\frac{π}{180})≒\sin\displaystyle\frac{π}{6}+\cos\displaystyle\frac{π}{6}\cdot(-\displaystyle\frac{π}{180})\)
\(=\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}\cdot\displaystyle\frac{π}{180}\)
\(≒0.485\)
よって
\(\sin(29°)≒0.485\)
(解答2)
\(\sin(29°)=\sin(30°-1°)=\sin(\displaystyle\frac{π}{6}-\displaystyle\frac{π}{180})\)
\(f(x)=\sin(\displaystyle\frac{π}{6}-x)\) とおくと
\(f'(x)=-\cos(\displaystyle\frac{π}{6}-x)\)
\(f(x)≒f(0)+f'(0)x\) (\(x\)は\(0\)に近い)
において、\(x=\displaystyle\frac{π}{180}\) を代入して
\(f(\displaystyle\frac{π}{180})≒\sin\displaystyle\frac{π}{6}-\cos\displaystyle\frac{π}{6}\cdot\displaystyle\frac{π}{180}\)
\(=\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}\cdot\displaystyle\frac{π}{180}\)
\(≒0.485\)
したがって
\(\sin(29°)=f(\displaystyle\frac{π}{180})\)\(≒0.485\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→微小変化量 back→変化率