曲線の曲がり具合

曲線の曲がり具合(曲率)と曲率円について見ていきます。
今回は例題で先に具体例を扱って、そのあとに一般論について検討したいと思います。

(例題)
\(xy\)平面において、曲線 \(C:y=\log x\) 上に2点 \(A(a,\log a)\)、\(B(a+h,\log(a+h))\)  (\(h≠0\)) をとる。点\(A\)における\(C\)の法線と点\(B\)における\(C\)の法線の交点を \(D(α,β)\) とする。

(1)点\(A\)における法線の方程式を求めよ。
(2)\(α\)と\(β\)をそれぞれ\(a\)と\(h\)を用いて表せ。
(3)\(p=\displaystyle\lim_{h \to 0}α\) と \(q=\displaystyle\lim_{h \to 0}β\) とする。\(p\)と\(q\)をそれぞれ\(a\)を用いて表せ。
(4)点\(E\)の座標を\((p,q)\)とする。線分\(AE\)の長さを最小にする\(a\)の値と、そのときの線分\(AE\)の長さを求めよ。

(解答)
(1)
(法線は接線に直交する接点を通る直線です)
\(C:y=\log x\)  (\(x>0\))
微分して
\(y’=\displaystyle\frac{1}{x}\)

よって \(A(a,\log a)\) における法線は、傾きが\(-a\)だから
\(y=-a(x-a)+\log a\)
\(y=-ax+a^2+\log a\)

(2)

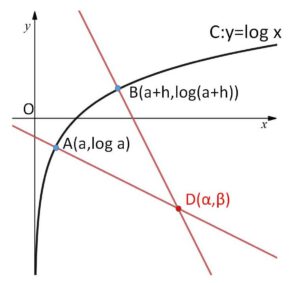
\(A(a,\log a)\) における法線は
\(y=-ax+a^2+\log a\)・・・①

\(B(a+h,\log(a+h))\) における法線は、①で\(a\)を\(a+h\)におきかえて
\(y=-(a+h)x+(a+h)^2+\log(a+h)\)・・・②

\(D(α,β)\)は①②の交点なので、①②を連立して\(x,y\)を求めればよい。
\(y\)を消去すると
\(-ax+a^2+\log a=-(a+h)x+(a+h)^2+\log(a+h)\)

\(hx=2ah+h^2+\log(a+h)-\log a\)
よって
\(x=α=2a+h+\displaystyle\frac{\log(a+h)-\log a}{h}\)

これを①に代入して
\(y=β\)\(=-a\{2a+h+\displaystyle\frac{\log(a+h)-\log a}{h}\}+a^2+\log a\)

\(=-a^2-ah+\log a-a\cdot\displaystyle\frac{\log(a+h)-\log a}{h}\)

(3)

\(p=\displaystyle\lim_{h \to 0}α\)

\(=\displaystyle\lim_{h \to 0}\{2a+h+\displaystyle\frac{\log(a+h)-\log a}{h}\}\)

(\(f(x)=\log x\)) とおくと

\(=\displaystyle\lim_{h \to 0}\{2a+h+\displaystyle\frac{f(a+h)-f(a)}{h}\}\)

\(=2a+f'(a)\)

\(=2a+\displaystyle\frac{1}{a}\)

同様に
\(q=\displaystyle\lim_{h \to 0}β\)

\(=\displaystyle\lim_{h \to 0}\{-a^2-ah+\log a-a\cdot\displaystyle\frac{\log(a+h)-\log a}{h}\}\)

\(=-a^2+\log a-af'(a)\)

\(=-a^2+\log a-1\)

(4)

\(A(a,\log a)\)
\(E(2a+\displaystyle\frac{1}{a},\ -a^2+\log a-1)\)
より

\(AE^2=(a+\displaystyle\frac{1}{a})^2+(-a^2-1)^2\)

\(=(\displaystyle\frac{a^2+1}{a})^2+(a^2+1)^2\)

\(=(a^2+1)^2(\displaystyle\frac{1}{a^2}+1)\)

\(=\displaystyle\frac{(a^2+1)^3}{a^2}\)

(\(a^2\)の関数になっているので、\(a^2=t\) とおきえると楽)

ここで \(a^2=t\) とおくと
\(a>0\) より \(t>0\) で
\(g(t)=\displaystyle\frac{(t+1)^3}{t}\) について

\(g'(t)=\displaystyle\frac{3(t+1)^2\cdot t-(t+1)^3\cdot1}{t^2}\)

\(=\displaystyle\frac{(t+1)^2(2t-1)}{t^2}\)

よって \(t=\displaystyle\frac{1}{2}\)　(\(a=\displaystyle\frac{1}{\sqrt{2}}\))　のとき
\(AE^2\) は最小値をとり、\(AE>0\) よりこのとき\(AE\)も最小となる。

\(AE\)の最小値は
\(AE=\sqrt{\displaystyle\frac{(\displaystyle\frac{1}{2}+1)^3}{\displaystyle\frac{1}{2}}}=\sqrt{\displaystyle\frac{27}{4}}\)

\(=\displaystyle\frac{3\sqrt{3}}{2}\)

(参考)曲率円

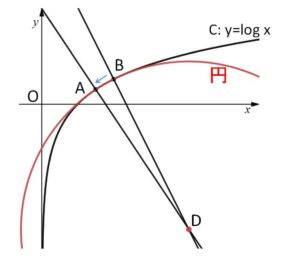
例題において、点\(B\)が点\(A\)に十分近いとき、中心をほとんど法線の交点\(D\)とする\(A,B\)を通る円を描くことができます。そして(3)では\(B\)を\(A\)に限りなく近づけたときの\(D\)の極限を考えているので、このとき\(D\)を中心とした半径\(AD\)の円を描くと点\(A\)付近ではこの円が曲線\(C\)を近似していることになり、点\(A\)における法線上に中心\(D\)があるので、点\(A\)で \(C:y=\log x\) で接していることになります。そしてこの極限状態の円を曲率円、その半径\(R\)を曲率半径、\(R\)の逆数\(\displaystyle\frac{1}{R}\)を曲率とびます。
球状である地球上にいる我々がほとんどその曲がり具合を気にしないように、円の半径が大きいほどその曲がり具合(曲率)は小さく、また円の半径が小さいほど曲率が大きくなります。したがって曲率の大小がそのまま曲線の曲がり具合の大小を表していることになります。

それでは、一般的に曲率円の方程式(円の中心の座標と半径)がどうなるか求めてみます。

\(f(x)\)が2回微分可能な関数であるとき、例題と同じ方針でいくと、
\(y=f(x)\) 上の2点\(A(a,f(a))\)、\(B(a+h,f(a+h))\) における法線はそれぞれ

\((x-a)+f'(a)(y-f(a))=0\)・・・(i)
\((x-(a+h))+f'(a+h)(y-f(a+h))=0\)・・・(ii)
(\(f'(x)=0\)の場合もあるので、この形式にした)

となる。法線の交点の\(y\)座標は、(i)－(ii)より\(x\)を消去して
\(h+\{f'(a)-f'(a+h)\}y-f'(a)f(a)+f'(a+h)f(a+h)=0\)
より
\(y=\displaystyle\frac{h-f'(a)f(a)+f'(a+h)f(a+h)}{f'(a+h)-f'(a)}\)

よって \(h \to 0\) の極限は
\(\displaystyle\lim_{h \to 0}y\)
\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{h-f'(a)f(a)+f'(a+h)f(a+h)}{f'(a+h)-f'(a)}\)

(分母分子\(h\)で割って)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{1+\displaystyle\frac{-f'(a)f(a)+f'(a+h)f(a+h)}{h}}{\displaystyle\frac{f'(a+h)-f'(a)}{h}}\)

(余分なものを足し引きすると)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{1+\displaystyle\frac{\color{blue}{f'(a)f(a+h)}-f'(a)f(a)+f'(a+h)f(a+h)\color{blue}{-f'(a)f(a+h)}}{h}}{\displaystyle\frac{f'(a+h)-f'(a)}{h}}\)

\(=\displaystyle\lim_{h \to 0}\displaystyle\frac{1+\displaystyle\frac{f(a+h)-f(a)}{h}\cdot f'(a)+\displaystyle\frac{f'(a+h)-f'(a)}{h}\cdot f(a+h)}{\displaystyle\frac{f'(a+h)-f'(a)}{h}}\)

\(=\displaystyle\frac{1+\{f'(a)\}^2+f”(a)f(a)}{f”(a)}\)

\(=f(a)+\displaystyle\frac{1+\{f'(a)\}^2}{f”(a)}\)　(曲率円の中心の\(y\)座標)

\(x\)座標については、これと(i)より
\(\displaystyle\lim_{h \to 0}x\)
\(=\displaystyle\lim_{h \to 0}\{a-f'(a)(y-f(a))\}\)

\(=a-f'(a)\cdot\displaystyle\frac{1+\{f'(a)\}^2}{f”(a)}\)  (曲率円の中心の\(x\)座標)

したがって曲率半径\(R\)は、\(A(a,f(a))\)との距離を考えて
\(R^2=\left\{f'(a)\cdot\displaystyle\frac{1+\{f'(a)\}^2}{f”(a)}\right\}^2+\left\{-\displaystyle\frac{1+\{f'(a)\}^2}{f”(a)}\right\}^2\)

\(=\{\{f'(a)\}^2+1\}\left\{\displaystyle\frac{1+\{f'(a)\}^2}{f”(a)}\right\}^2\)

\(=\displaystyle\frac{\{1+\{f'(a)\}^2\}^3}{\{f”(a)\}^2}\)
より

\(R=\displaystyle\frac{\{1+\{f'(a)\}^2\}^{\frac{3}{2}}}{|f”(a)|}\)
となります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→2次以上の近似式