データの分析に関する知識は、大学で実験をする学部を筆頭にとても重要になってきます。また日常生活においても例えば天気予報の降水量や気温などの表示にもこの分野の考え方が使われています。
・度数分布表
学校のテストの点数を例に挙げます。16人の生徒全員の名前を決めるのは大変なので、文字で表させてください。
A先生のクラスの生徒は16人である。このクラスの生徒が数学のテストを受験したとき、その結果を\(x_i\)とすると \((i=1,2・・・16)\) 次のようになった。
\(x_1=62,x_2=76,x_3=42,x_4=55\)
\(x_5=96,x_6=88,x_7=35,x_8=63\)
\(x_9=82,x_{10}=48,x_{11}=51,x_{12}=58\)
\(x_{13}=61,x_{14}=84,x_{15}=69,x_{16}=76\)
\(x_1=62,x_2=76,x_3=42,x_4=55\)
\(x_5=96,x_6=88,x_7=35,x_8=63\)
\(x_9=82,x_{10}=48,x_{11}=51,x_{12}=58\)
\(x_{13}=61,x_{14}=84,x_{15}=69,x_{16}=76\)
このままでは分かりにくいので、A先生はテストの結果を整理しようと考えて10点区切りのグループに分けて表にしました。
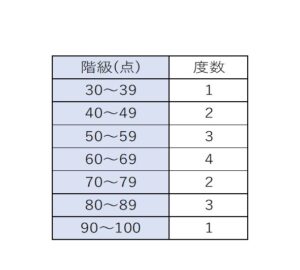
30点~39点、40点~49点・・・のようにグループ化された区間を階級、そして各階級に含まれるデータの個数を度数といいます。この例では度数は各階級に含まれる人数のことで、つまり30点~39点の人は1人、40点~49点の人は2人・・・いるということです。この表のように階級を設定して度数を対応させた表を度数分布表といいます。
また、階級の区間の幅を階級幅、各階級の真ん中の値を階級値といいます。例では階級幅は10、階級値は例えば50点~59点の場合は、\(\displaystyle\frac{50+59}{2}=\)54.5点となります。
ある特性を数量的に表すものを変量といいます。この例では変量はテストの点数です。また、変量の測定値を集めたものをデータとよびます。16人分のテストの具体的な点数がデータですね。さらにデータを構成する測定値の個数をデータの大きさといいます。個数は16なのでデータの大きさは16となります。
・ヒストグラム
度数分布表をもとに視覚的に分かりやすく柱上のグラフにしたものをヒストグラムといいます。
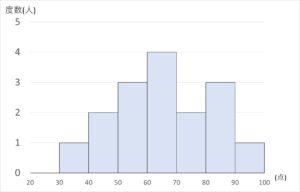
グラフにすると分かりやすいですね。各長方形の高さは各階級の度数であり、面積は度数に比例しています。
・相対度数
各階級の度数の全体に対する割合を相対度数といいます。例での30点~39点での度数は1で全体の度数は16なので、階級30点~39点の相対度数は、\(\displaystyle\frac{1}{16}≒0.063\) となります。他の階級でも同様な計算をして、各階級に相対度数を対応させた作った表を相対度数分布表といいます。
各階級の度数の全体に対する割合を相対度数といいます。例での30点~39点での度数は1で全体の度数は16なので、階級30点~39点の相対度数は、\(\displaystyle\frac{1}{16}≒0.063\) となります。他の階級でも同様な計算をして、各階級に相対度数を対応させた作った表を相対度数分布表といいます。
・累積度数と累積相対度数
最初の階級からその階級まで度数を合計したものを累積度数、またその階級までの相対度数を合計したものを累積相対度数といいます。例のテストの点数では、30点~39点の累積度数は1、40点~49点の累積度数は1+2=3、50点~59点の累積度数は1+2+3=6、と和を積み重ねて計算すればよいです。累積相対度数も同様に相対度数を積み重ねても計算できますし、累積度数を全体の度数で割ってもよいです。
最初の階級からその階級まで度数を合計したものを累積度数、またその階級までの相対度数を合計したものを累積相対度数といいます。例のテストの点数では、30点~39点の累積度数は1、40点~49点の累積度数は1+2=3、50点~59点の累積度数は1+2+3=6、と和を積み重ねて計算すればよいです。累積相対度数も同様に相対度数を積み重ねても計算できますし、累積度数を全体の度数で割ってもよいです。
最後に相対度数と累積度数と累積相対度数を合わせた表を出しておきます。
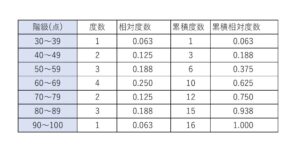
相対度数は全体に対する割合をみるとき、累積度数は積み重ねた量を知りたいとき(例えば累計の降水量を調べたいときなど)に便利です。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。