具体的に代表値に関する問題を解いていきます。
(問題)
30人のクラスで10点満点のテストを行い、その結果は次の通りである。
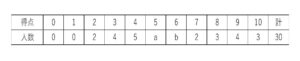
(1)\(a+b\) の値を求めよ。
(2)得点の平均値が\(6\)点のとき、\(a\)と\(b\)の値の組\((a,b)\)を求めよ。
(3)得点の中央値が\(5.5\)点のとき、\(a\)と\(b\)の値の組\((a,b)\)を求めよ。
(解答)
(1)合計の人数が\(30\)人だから
\(2+4+5+a+b+2+3+4+3=30\)
よって \(a+b=7\)
(2)平均値が\(6\)点だから
\(\displaystyle\frac{1}{30}(2×2+3×4+4×5+5a+6b\)
\(+7×2+8×3+9×4+10×3)=6\)
\(140+5a+6b=180\)だから
\(5a+6b=40\)・・・①
(1)より \(a+b=7\)・・・② だから①②を連立すると
\((a,b)=(2,5)\)
(3)
クラスの人数が偶数で、5と6の平均が中央値になっているので、テストの得点を小さい数から並べて15番目が5点、16番目が6点となります。なので5点までの人数の合計が15人です。(6点以上の人数も15人です)
得点の中央値が\(5.5\)点なので、得点を小さい順にならべて15番目が\(5\)点,16番目が\(6\)点となる。よって\(5\)点以下の人数が\(15\)人となるので
\(2+4+5+a=15\)
ゆえに \(a=4\) (1)より\(a+b=7\) だから \(b=3\)
\((a,b)=(4,3)\)
\(2+4+5+a=15\)
ゆえに \(a=4\) (1)より\(a+b=7\) だから \(b=3\)
\((a,b)=(4,3)\)
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。