箱ひげ図の読み取り | 教えて数学理科

箱ひげ図からどんなことが読み取れるでしょうか。

(例題)

次の図は、ある学校の1年生、2年生各200人の身長のデータの箱ひげ図である。この図から読み取れることとして正しいものをすべて選べ。

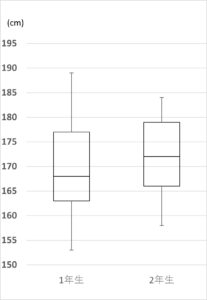
箱髭図の読み取り

(1)\(185cm\)より大きい生徒が1年生にはいるが、2年生にはいない。
(2)\(170cm\)以上の生徒が1年生では100人以下であるが、2年生では100人以上いる。
(3)\(165cm\)以下の生徒がどちらの学年にも50人より多くいる。
(4)\(175cm\)以下の生徒は1年生では150人より多くいるが、2年生では150人以下である。
(5)1年生のデータの範囲は、2年生のデータの範囲より\(20cm\)以上大きい。

どんな箱ひげ図でも、最小値,四分位数(\(Q_1,Q_2,Q_3\)),最大値の5つの量は読み取れます。また、今回の問題ではデータの個数が1年生、2年生でそれぞれ200個なので、四分位数で4等分された各ブロックではそれぞれ50個ずつのデータが存在することになります。中央値は偶数個を半分にわけるので100番目と101番目の平均、\(Q_1,Q_3\)も偶数個(100個)を半分にわけるのでどちらも2つの数(50番目と51番目、150番目と151番目)の平均値となります。

(解答)

(1)
1年生の身長の最大値\(M\)は、\(M>185\)
2年生の身長の最大値\(M’\)は、\(M'<185\)
よって正しい。

(2)
1年生の身長の中央値は 170より小さい。少なくとも100人は170cmより小さいことになるので、170cm以上の生徒は100人以下となる。
2年生の身長の中央値は170より大きい。少なくとも100人は170cmより大きいことになるので、170cm以上の生徒は100人以上となる。
よって正しい。

(3)
1年生の身長の\(Q_1\)は165より小さい。少なくとも50人は165cmより小さいことになるので165cm以下の生徒は50人以上となる。
2年生の身長の\(Q_2\)は165より大きい。165cm以下の生徒は多くても50人なので、165cm以下の生徒は50人以下となる。
よって正しくない。

(4)
1年生の身長の\(Q_3\)は175より大きい。175cm以下の生徒は多くても150人になるので、175cm以下の生徒は150人以下となる。
2年生の身長の\(Q_3\)は175より大きい。175cm以下の生徒は多くても150人になるので、175cm以下の生徒は150人以下となる。
よって正しくない。

(5)
それぞれの学年の最大値について
\(185<M<190\),　\(180<M'<185\)
それぞれの学年の最小値について1年生は\(m\),2年生は\(m’\)とすると
\(150<m<155\),　\(155<m'<160\)

\(30<M-m<40\) ,\(20<M’-m'<30\)　となるので
1年生のデータの範囲は30から40,2年生のデータの範囲は20から30の間の値となるので20cm以上大きくはならない。
よって正しくない。

\(M-m\)の範囲を出すときは辺々を単純に差をとってはいけません。(\(185-150<M-m<190-155\)とはならない)
－1をかけて \(-150>-m>-155\) だから\(-155<-m<-150\)として符号の向きを変化させてから和　\(185-155<M-m<190-150\)　をとります。

他にも箱ひげ図からは散らばりがわかります。全体の散らばりをみると範囲が大きい1年生のほうが散らばりが大きいことになります。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→分散と標準偏差　 back→四分位数と箱ひげ図