相関係数 | 教えて数学理科

前回は散布図と相関関係について学びましたが、今回は相関関係を数値で表す方法について学びます。

具体的な数値で表すことで、相関関係をより分かりやすくします。

・共分散
相関関係を数値化するために次のように共分散($s_{xy}$)を定義します。

2つの変量$x,y$の$n$個のデータを、$(x_1,y_1),(x_2,y_2),・・・(x_{n},y_{n})$ とし、$x,y$の平均値をそれぞれ$\bar{x},\bar{y}$とするとき、$x,y$の平均値からの偏差の積の平均を共分散とします。つまり

$s_{xy}=\displaystyle\frac{1}{n}\{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+$
$・・・+(x_{n}-\bar{x})(y_{n}-\bar{y})\}$

となります。

共分散$s_{xy}$が正の値のときは、図で+の部分に多くの点が分布していることになるので正の相関関係があることになり、負の値ときは図で－の部分に多くの点が分布していることになるので負の相関関係があることになります。

共分散

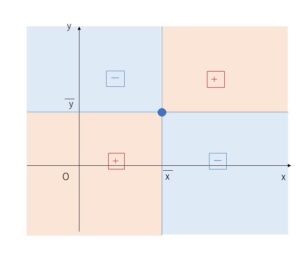
ただ共分散は点の分布の平均値からの散らばりが大きいと、その絶対値がいくらでも大きくなってしまうので散らばりも考慮した量(相関係数)を新たに定義します。
その前に共分散の公式を1つ紹介します。

[共分散の公式]
$xy$の平均値を$\overline{xy}$とすると、$s_{xy}=\overline{xy}-\bar{x}\bar{y}$

(証明)
$s_{xy}=\displaystyle\frac{1}{n}\{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+$
$・・・+(x_{n}-\bar{x})(y_{n}-\bar{y})\}$

$=\displaystyle\frac{1}{n}\{(x_1y_1+x_2y_2+・・・+x_{n}y_{n})$
$-\bar{y}(x_1+x_2+・・・+x_{n})$
$-\bar{x}(y_1+y_2+・・・y_{n})+n・\bar{x}\bar{y}\}$

$=\overline{xy}-\bar{x}\bar{y}-\bar{x}\bar{y}+\bar{x}\bar{y}$

$=\overline{xy}-\bar{x}\bar{y}$

・相関係数
$x,y$の標準偏差$s_x,s_y$と共分散$s_{xy}$を用いて相関係数$r_{xy}$を次のように定義します。

$r_{xy}=\displaystyle\frac{s_{xy}}{s_xs_y}$

共分散をそれぞれの変量の標準偏差で割って、散らばりを考慮するイメージです。

この定義により、相関係数には次のような性質があります。

①$-1≦r_{xy}≦1$であり、特に$r_{xy}=±1$のときはすべての点が1直線状に並び、この直線は$(\bar{x},\bar{y})$を通る。
②$r_{xy}$が$1$に近いほど強い正の相関、$-1$に近いほど強い負の相関となる。また、$0$に近いほど(直線的な)相関がなくなる。
③$r_{xy}$に単位はない。

(①について)
コーシー・シュワルツの不等式を用いて証明してみます。

(コーシー・シュワルツの不等式)
実数$a_1～a_{n},b_1～b_{n}$について

$(a_1^2+a_2^2+・・・+a_{n}^2)(b_1^2+b_2^2+・・・+b_{n}^2)$

$≧(a_1b_1+a_2b_2+・・・+a_{n}b_{n})^2$

等号成立は
$a_1k-b_1=a_2k-b_2=・・・=a_{n}k-b_{n}=0$　となる実数$k$が存在するときである。

(コーシー・シュワルツの不等式自体の証明は　(→コーシー・シュワルツの不等式(和の形)) を参照してください。)

(証明)
コーシー・シュワルツの不等式の両辺を$0$でない数$n^2$で割ると、
$\displaystyle\frac{1}{n}(a_1^2+a_2^2+・・・+a_{n}^2)・\displaystyle\frac{1}{n}(b_1^2+b_2^2+・・・+b_{n}^2)$
$≧\{\displaystyle\frac{1}{n}(a_1b_1+a_2b_2+・・・+a_{n}b_{n})\}^2$

$a_{i}=x_{i}-\bar{x}$,　$b_{i}=y_{i}-\bar{y}$　($i=1,2,・・・n$)として不等式に代入すると、$x,y$の分散を$s_{x}^2,s_{y}^2$として

$s_{x}^2s_{y}^2≧s_{xy}^2$

よって、$\displaystyle\frac{s_{xy}^2}{s_x^2s_y^2}≦1$ であり、$r_{xy}^2≦1$　だから $-1≦r_{xy}≦1$

等号成立時、つまり$r_{xy}=±1$のときは、$a_{i}k-b_{i}=0$となる$k$が存在するときで、このとき$(x_{i}-\bar{x})k-(y_{i}-\bar{y})=0$となるので、$y_{i}=k(x_{i}-\bar{x})+\bar{y}$・・・(※)

(※)は$(x_1,y_1),(x_2,y_2)・・・(x_{n},y_{n})$の全てが、直線$y=k(x-\bar{x})+\bar{y}$にあることを示す。またこの直線は$(\bar{x},\bar{y})$を通る。

(②について)
厳密な証明は高校の範囲を超えるので省略します。ざっくりとですが、相関係数が$1$に近づくとき、分子の共分散は正の値であり、相関係数の値を大きくするためには上図の+部分に点が多く分布することになるので正の相関が強くなり、$-1$に近づくとき、分子は負の値であり相関係数の値を小さくするためには－部分に点が多く分布することになるので負の相関が強くなります。$0$のときはどちらの傾向もみられないことになります。

(③について)

$x,y$の単位を$$,@$とすると、分子の単位は$$@$、分母の単位は$\sqrt{$^2}\sqrt{@^2}=$@$ であり相関係数の単位はありません。単位は分母分子で打ち消されるため、例えば一方を$cm$から$m$に単位変換しても相関係数の値は変わらないことになります。(詳しくは次回 (2-6)変量の変換② を参照してください)

色々長々と書きましたが、実際に例題を通して相関係数を求めてみます。計算は大変なことが多いですが機械的作業なので時間をかければ誰でもできるので頑張りましょう。

(例題)
次の表は、学生5名の身長$x(cm)$と体重$y(kg)$を測定した結果である。$x$と$y$の相関係数$r$を求めよ。

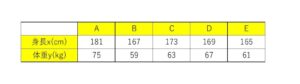
相関係数例題1

(解答)
$x,y$の平均値を$\bar{x},\bar{y}$とすると以下の表を得ることができる。
($\bar{x}=\displaystyle\frac{855}{5}=171$,　$\bar{y}=\displaystyle\frac{325}{5}=65$)

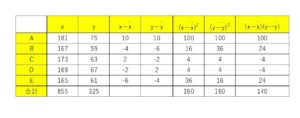
よって

$r=\displaystyle\frac{\displaystyle\frac{140}{5}}{\sqrt{\displaystyle\frac{160}{5}}\sqrt{\displaystyle\frac{160}{5}}}=\displaystyle\frac{140}{\sqrt{160}\sqrt{160}}=\displaystyle\frac{140}{160}=$$0.875$

データ数$n$は約分されるので、和だけを考えても構いません。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→変量の変換②　back→散布図と相関