実数・純虚数条件

共役複素数を利用した実数・純虚数条件や、共役複素数による実部と虚部の表記方法について見ていきます。一応純虚数の定義のおさらいをしておきます。

・共役複素数による実数・純虚数の判定方法

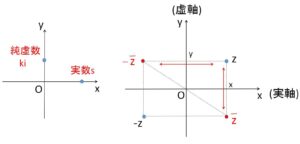
複素数平面上で実数は実軸について対称移動しても位置は変わらない、また純虚数は虚軸について対称移動しても変わらないことから、次のことが成り立ちます。

(2)の\(z≠0\)は \(z=0\) (実数) を除くためです。また \(z=-\bar{z}\) は \(z+\bar{z}=0\) とすることもあります。

なお(1)(2)を丁寧に証明すると次のようになります。

(1)\(→\)について
\(z=s\) (\(s\)は実数) とおけるので
\(\bar{z}=\bar{s}=s=z\)
\(←\)について
\(z=a+bi\) とおくと \(z=\bar{z}\) より
\(a+bi=a-bi\)
\(2bi=0\)
よって \(b=0\) だから、\(z\)は実数となる。

(2)\(→\)について
\(z=ki\) (\(k\)は\(0\)でない実数) とおけるので
\(-\bar{z}=-(-ki)=ki=z\)
また \(k≠0\) より \(z≠0\)
\(←\)について
\(z=a+bi\) とおくと \(z=-\bar{z}\) より
\(a+bi=-(a-bi)\)
よって
\(a=0\)
また \(z≠0\) より \(b≠0\) となるので、\(z\)は純虚数である。

・共役複素数と実部・虚部
複素数
\(z=a+bi\)・・・①
の実部\(a\)、虚部\(b\)を共役複素数
\(\bar{z}=a-bi\)・・・②
を用いて表すことができます。連立方程式を解く要領で
(①+②)÷2 より
\((zの実部)=a=\displaystyle\frac{z+\bar{z}}{2}\)・・・③

(①－②)÷2i より
\((zの虚部)=b=\displaystyle\frac{z-\bar{z}}{2i}\)・・・④

よって③④により成分\(a,b\)を用いずに、複素数\(z,\bar{z}\)のまま実部・虚部を扱えることが可能になります。
また任意の複素数\(z\)について
\(z+\bar{z}\) は実数
\(z-\bar{z}\) は純虚数または\(0\)
となることも分かります。

なお\(a,b\)が\(0\)かどうかが実数・純虚数になるかの基準になるので、③④から上記の実数・純虚数条件を導くこともできます。

(例題)
\(α,β\)はともに\(0\)でない複素数とする。このとき\(\bar{α}β\)が実数であれば、\(β\)は\(α\)の実数倍であることを証明せよ。

(解答1)複素数のまま
\(\bar{α}β\)が実数なので
\(\bar{α}β=\overline{\bar{α}β}\)
よって
\(\bar{α}β=α\bar{β}\)
\(α≠0\) より \(\bar{α}≠0\) だから
\(\displaystyle\frac{β}{α}=\displaystyle\frac{\bar{β}}{\bar{α}}\)
\(\displaystyle\frac{β}{α}=\overline{(\displaystyle\frac{β}{α})}\)

ゆえに、\(\displaystyle\frac{β}{α}=k\)　(\(k\)は実数) となるから
\(β=kα\)
つまり、\(β\)は\(α\)の実数倍となる。

(解答2)\(a+bi\) とおく
\(α=a+bi\)、\(β=c+di\) とおくと

\(\bar{α}β=(a-bi)(c+di)\)
\(=(ac+bd)+(ad-bc)i\)

\(\bar{α}β\)は実数だから
\(ad-bc=0\)・・・①

よって2つのベクトル \((a,b),\ (c,d)\) は平行となるから、複素数平面上で3点 \(0,α,β\) は1直線上にあり
\(β=kα\) (\(k\)は実数)
と表される。つまり、\(β\)は\(α\)の実数倍となる。

(注)
①より
\(\displaystyle\frac{a}{b}=\displaystyle\frac{c}{d}\)　(\(a:b=c:d\))
となりますが、\(b,d\)が\(0\)になる可能性もあるので(虚部が\(0\)になることはあり得る。このとき実部は\(0\)ではない)、ベクトルで処理して場合分けを避けました。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数の絶対値　back→複素数平面と共役複素数