複素数の絶対値の定義とその演算について見ていきます。
・複素数の絶対値
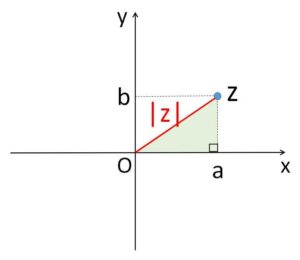
複素数平面上で点\(z\)と原点\(O\)の距離を、複素数\(z\)の絶対値とよび、\(|z|\)で表します。
よって \(z=a+bi\) とおくと、座標平面上における \((0,0)\) と \((a,b)\) の距離を考えて
\(|z|=|a+bi|=\sqrt{a^2+b^2}\)
またこの定義により絶対値について次の性質が成り立つことになります。
(1)\(|z|≧0\) (常に\(0\)以上の実数)
特に \(|z|=0\) \(⇔\) \(z=0\)
(2)\(|z|=|\bar{z}|=|-z|=|-\bar{z}|\)
(3)\(z\bar{z}=|z|^2\) (\(\sqrt{z\bar{z}}=|z|\))
(4)\(|αβ|=|α||β|\)
特に \(|α^2|=|α|^2\)、\(|α^n|=|α|^n\)
(5)\(\left|\displaystyle\frac{α}{β}\right|=\displaystyle\frac{|α|}{|β|}\) (ただし\(β≠0\))
(解説)
ざっくりとその内容を説明すると
(1)\(|z|\)は原点\(O\)との距離なので\(0\)以上。
特に \(|z|=0\) になるときは、\(z=0\) に限られる。
(2)\(z\)との対称性より、\(z,\bar{z},-z,-\bar{z}\) の絶対値は全て同じ。
(3)共役複素数同士の積は絶対値の2乗になる。(共役複素数と絶対値の変換公式になる)
(4)(5)ばらばらに絶対値をとって計算してもよい。
これらはすべて \(z=a+bi\) などとおけば証明できます((4)の\(n\)乗は帰納法を用いる)。
特に重要なのが共役複素数と絶対値の関係(変換)を表す(3)の
\(z\bar{z}=|z|^2\)
でこれを証明すると
\(z\bar{z}=(a+bi)(a-bi)\)
\(=a^2+b^2\)
\(=|z|^2\)
したがって、\(z\bar{z}\)は常に実数でしかも\(0\)以上の値になります。
また例えば \(|z|=2\) のような条件式が与えられている場合
\(|z|^2=4\) (2乗するのがポイント)
\(z\bar{z}=4\)
\(|z|=2\) より \(z≠0\) だから
\(\bar{z}=\displaystyle\frac{4}{z}\)
となり、\(\bar{z}\)を消去する式が得られこれも重要です。
・2点間の距離(複素数平面)
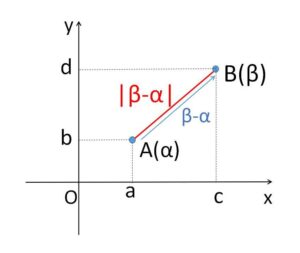
複素数平面上の 2点 \(A(α),B(β)\) の距離は
\(AB=|β-α|\) \((=|α-β|)\)
\(β-α\) は \(\overrightarrow{AB}\) を表しているので\(A\)を原点のように扱えばその大きさが距離になるということですが、式で証明すると次の通りです。
\(α=a+bi\)、\(β=c+di\) とおくと
\(|β-α|=|(c-a)+(d-b)i|\)
\(=\sqrt{(c-a)^2+(d-b)^2}\) (座標平面での\(AB\)の距離)
(例題)
複素数\(α,β\)について、
\(|α|=|β|=2\)、\(α+β+2=0\)
であるとき、\(αβ\)の値を求めよ。
(解答1)\(\bar{α},\bar{β}\)を消去
\(|α|=|β|=2\) より
\(|α|^2=|β|^2=4\)
\(α\bar{α}=β\bar{β}=4\)
よって
\(\bar{α}=\displaystyle\frac{4}{α}\)、\(\bar{β}=\displaystyle\frac{4}{β}\)・・・①
また
\(α+β+2=0\)・・・②
の両辺で共役複素数をとると
\(\overline{α+β+2}=\bar{0}\)
\(\bar{α}+\bar{β}+2=0\)・・・③
③に①を代入して
\(\displaystyle\frac{4}{α}+\displaystyle\frac{4}{β}+2=0\)
\(\displaystyle\frac{4(α+β)}{αβ}+2=0\)
②より
\(\displaystyle\frac{-8}{αβ}+2=0\)
したがって
\(αβ=4\)
(注)
\(α+β=-2\) なので、\(αβ=4\)とあわせて具体的に\(α,β\)の値を求めることができます。
(解答2)\(β\)を消去
\(|α|=|β|=2\)・・・(1)
\(α+β+2=0\)・・・(2)
(2)より
\(β=-(α+2)\)
これを(1)に代入して
\(|α|=|-(α+2)|=2\)
\(|α|=2\) より
\(|α|^2=4\) だから
\(α\bar{α}=4\)・・・(3)
また
\(|α|=|α+2|\) より
\(|α|^2=|α+2|^2\)
\(α\bar{α}=(α+2)\overline{(α+2)}\) (この展開が大事)
\(α\bar{α}=(α+2)(\bar{α}+2)\)
\(α\bar{α}=α\bar{α}+2α+2\bar{α}+4\)
よって
\(α+\bar{α}=-2\)・・・(4)
(3)(4)より
\(α,\bar{α}\)は、2次方程式
\(x^2+2x+4=0\)
の解だから
\(α^2+2α+4=0\)・・・(5)
したがって
\(αβ=-α(α+2)\)
\(=-α^2-2α\)
\(=4\) ((5)より)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→実数係数のn次方程式 back→実数・純虚数条件