ド・モアブルの定理を利用した \(z^n=1\) の解を求める方法について見ていきます。
・\(z^n=1\) の解
最終的な目標は \(z^n=α\) (\(α\)は複素数) の解を求めることですが、まずは \(z^n=1\) の解から始めて段階を踏んでいきます。
\(n\)が小さい自然数の場合、例えば \(z^2=1\) や \(z^3=1\) などは因数分解で求めることができますが、\(z^{20}=1\) のような大きな\(n\)の場合には大変です。そこでド・モアブルの定理を利用すると、\(z^n=1\) の解をスッキリ求めることが可能です。
\(z^n=1\)・・・① の解を
\(z=r(\cosθ+i\sinθ)\) (\(r>0\))
とおいて①に代入すると
\(r^n(\cos nθ+i\sin nθ)=1(\cos0+i\sin0)\)
よって
\(r^n=1\)、\(nθ=0+2kπ\) (\(k\)は整数)
となるから
\(r=1\)・・・(注1)
\(θ=\displaystyle\frac{2kπ}{n}\)
よって①の解は
\(z=\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\)・・・②
で表されます。ここで、\(k\)を\(0\)スタートとして
\(k=0,1,2,\cdots,n-1\) (全部で\(n\)個)
まで動かすと、解②はすべて異なる複素数を表し(注2)、①の解は高々\(n\)個なので全ての解が出揃うことになります。
したがって \(z^n=1\) の解(の全て)は
\(z_{k}=\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\) (\(k=0,1,2,\cdots,n-1\))
また、これらの解は\(n\)乗すると\(1\)になるので\(1\)の\(n\)乗根と呼ばれます。
なお、例えば \(k=n\) や \(k=-1\) の場合などはどうなるかというと
\(k=n\) のとき
\(z=\cos2kπ+i\sin2kπ=\cos0+i\sin0\)
より、\(k=0\) と同じ。
\(k=-1\) のとき
\(z=\cos(\displaystyle\frac{-2π}{n})+i\sin(\displaystyle\frac{-2π}{n})\)
(偏角を\(+2π\)して)
\(=\cos\displaystyle\frac{2(n-1)π}{n}+i\sin\displaystyle\frac{2(n-1)π}{n}\)
より、\(k=n-1\)と 同じ。つまり、重複がでてきます。
これらのことは、複素数平面上の単位円に内接する正多角形の頂点と対応させると分かりやすいと思います。(下記参照)
(注1)
\(r=1\) は \(r^n=1\) から求めましたが、これはまさに \(z^n=1\) の解を求めているような気がするかもしれません。しかし\(z\)と違って、\(r\)は正の実数なので \(r^n=1\) を満たすのは \(r=1\) とただ1つに決まります。(\(f(x)=x^n\) のグラフなどを考えるとよい)
(注2)
\(k=0,1,2,\cdots,n-1\) とした場合の解②が全て異なることは②を複素数平面上に図示するとよりはっきりとします。(下記参照)
・\(z^n=1\) の解と正多角形
\(z^n=1\) の解
\(z_{k}=\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\) (\(k=0,1,2,\cdots,n-1\))
を複素数平面に図示してみます。これらの解は \(r=1\) より単位円上にあり、偏角に着目すると
\(θ=\displaystyle\frac{2π}{n},\displaystyle\frac{4π}{n},\displaystyle\frac{6π}{n},\cdots,\displaystyle\frac{2(n-1)π}{n}\)
により、隣り合う動径がなす角は全て\(\displaystyle\frac{2π}{n}\)であり、中心角1周分\(2π\)を\(n\)等分しているので、円弧を\(n\)等分するところに位置しています。
よって解である\(n\)個の複素数を線分で結ぶと正\(n\)角形を描くことになり、この正多角形は単位円に内接することになります。
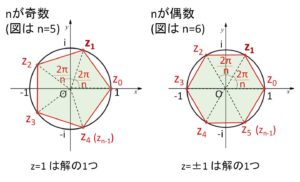
また最も小さい正の偏角をもつ解は
\(z_1=\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n}\)
であり、\(z_1\)倍すると複素数平面上では \(+\displaystyle\frac{2π}{n}\) の回転移動(拡大縮小はなし)をすることから、\(z^n=1\) の各解\(z_k\)は\(z_1\)を用いて
\(z_k=z_1^k\)
と表すことが可能です。これは次のように式で考えることもできます。
\(z_k=\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\)
\(=(\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n})^k\)
\(=z_1^k\)
・\(z^n=a\) (\(a\)は正の実数) の解
ほとんど \(z^n=1\) の場合と同じで、しかも一般化した \(z^n=α\) (\(α\)は複素数) に含めてもよいですが、ざっくりと扱いたいと思います。
\(z^n=a\)・・・(1) (\(a\)は正の実数)
の解を \(z=r(\cosθ+i\sinθ)\) (\(r>0\))
とおくと、(1)に代入して
\(r^n(\cos nθ+i\sin nθ)=a(\cos0+i\sin0)\)
よって
\(r^n=a\)、\(nθ=2kπ\) (\(k\)は整数)
となり、\(r=\sqrt[n]{a}\) となる以外は \(z^n=1\) と同様になります。
したがって(1)の解は
\(z_{k}=\sqrt[n]{a}\left(\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\right)\) (\(k=0,1,2,\cdots,n-1\))
これらの複素数解を図示すると正\(n\)角形になりますが、外接円の半径は \(\sqrt[n]{a}\) となります。また、\(z_k\) を \(z^n=1\) の解の1つを用いて表すと
\(z_k=\sqrt[n]{a}\left(\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n}\right)\)
\(=\sqrt[n]{a}\left(\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n}\right)^{k}\)
\(=\sqrt[n]{a}\ ω^{k}\) (\(ω=\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n}\))
(この\(ω\)は、\(z^n=1\) の解の \(z_1\) と同じです。\(z^n=a\) の解 \(z_1\) とは違います)
(例題)
方程式 \(z^6=1\) を複素数の範囲で解け。
(解答)
\(z=r(\cosθ+i\sinθ)\) (\(r>0\)) とおくと
\(z^6=1\) より
\(r^6(\cos6θ+i\sin6θ)=1(\cos0+i\sin0)\)
よって
\(r^6=1\)、\(6θ=2kπ\) (\(k\)は整数)
となるから
\(r=1\)、\(θ=\displaystyle\frac{kπ}{3}\)
ゆえに
\(z=\cos\displaystyle\frac{kπ}{3}+i\sin\displaystyle\frac{kπ}{3}\)
\(k=0,1,2,3,4,5\) とすればよく、それぞれ\(k\)の値を代入すると方程式の解は
\(z=1,\ \displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i,\ -\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i,\)
\(-1,\ -\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i,\ \displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
(全部で6個)
(別解)
\(z^6=1\) より
\(z^6-1=0\)
(\((z^3)^2-1^2=0\) と見て)
\((z^3+1)(z^3-1)=0\)
\((z+1)(z^2-z+1)(z-1)(z^2+z+1)=0\)
2次式は解の公式を利用することで
\(z=±1,\ \displaystyle\frac{1±\sqrt{3}i}{2},\ \displaystyle\frac{-1±\sqrt{3}i}{2}\)
6次式くらいなら因数分解のほうが楽かもしれませんが、ド・モアブルの定理のよさは複素数平面との対応を考えることで、解の規則性(順番性)が分かることやその図形的に意味を捉えることができる点です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→z^n=α の解 back→ド・モアブルの定理と実数条件・整数問題