\(z^n=α\) (\(α\)は複素数) の解法について見ていきます。
・\(z^n=α\) の解
\(z^n=1\) の場合と同様に
\(z^n=α\)・・・① (\(α\)は\(0\)でない複素数)
の解も、ド・モアブルの定理を用いて求めることができます。
①の解を
\(z=r(\cosθ+i\sinθ)\)・・・② (\(r>0\))
とおくと、複素数\(α\)が極形式で \(α=R(\cosφ+i\sinφ)\) (\(R>0\)) で表されるとすると、②を①に代入して
\(r^n(\cos nθ+i\sin nθ)=R(\cosφ+i\sinφ)\)
よって
\(r^n=R\)、\(nθ=φ+2kπ\) (\(k\)は整数)
より
\(r=\sqrt[n]{R}\)、\(θ=\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n}\)
となるので、①に代入して
\(z_{k}=\sqrt[n]{R}\left\{\cos(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})+i\sin(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})\right\}\)・・・③
ここで、\(k=0,1,2,\cdots,n-1\) まで変化させると③はすべて異なる複素数になり(複素数平面上の正多角形を考えるとよい。下記参照)、方程式① \(z^n=α\) の解は高々\(n\)個なので、これで全ての解が出揃うことになります (\(k=n,n+1,\cdots\) とすると解はループします)。よって①の解は
\(z_{k}=\sqrt[n]{R}\left\{\cos(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})+i\sin(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})\right\}\)・・・③
(\(k=0,1,2,\cdots,n-1\))
これらは\(n\)乗すると\(α\)になることから、\(α\)の\(n\)乗根と呼ばれます。
さて解③を複素数平面に図示すると、解の絶対値は全て\(\sqrt[n]{R}\)だから半径\(\sqrt[n]{R}\)の円周上にあり、さらに隣り合う複素数の偏角の差は全て
\(\displaystyle\frac{φ}{n}+\displaystyle\frac{2(k+1)π}{n}-(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})=\)\(\displaystyle\frac{2π}{n}\)
となるため、\(n\)個の複素数を線分で結ぶと正\(n\)角形になり、半径\(\sqrt[n]{R}\)の円に内接します。ただし、\(z^n=1\) の場合と比べて角 \(\displaystyle\frac{φ}{n}\) の分だけ正多角形はズレています。
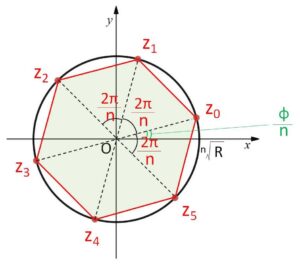
また、解の1つである\(k=0\)の場合の
\(z_0=\sqrt[n]{R}\left(\cos\displaystyle\frac{φ}{n}+i\sin\displaystyle\frac{φ}{n}\right)\)
と、\(1\)の\(n\)乗根の1つ
\(ω=\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n}\)
を用いると、\(z_k\)を次のように表すこともできます。
\(z_{k}=\sqrt[n]{R}\left\{\cos(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})+i\sin(\displaystyle\frac{φ}{n}+\displaystyle\frac{2kπ}{n})\right\}\)
\(=\sqrt[n]{R}(\cos\displaystyle\frac{φ}{n}+i\sin\displaystyle\frac{φ}{n})(\cos\displaystyle\frac{2kπ}{n}+i\sin\displaystyle\frac{2kπ}{n})\)
\(=z_0(\cos\displaystyle\frac{2π}{n}+i\sin\displaystyle\frac{2π}{n})^{k}\)
\(=z_0ω^{k}\)
(例題)
方程式 \(z^4+4=0\) を解け。
(解答)
\(z^4=-4\)
\(z^4=4(\cosπ+i\sinπ)\)
\(z=r(\cosθ+i\sinθ)\) (\(r>0\)) とおくと
\(r^4(\cos4θ+i\sinθ)=4(\cosπ+i\sinπ)\)
よって
\(r^4=4\)、\(4θ=π+2kπ\) (\(k=0,1,2,3\))
より
\(r=\sqrt{2}\)、\(θ=\displaystyle\frac{π}{4}+\displaystyle\frac{kπ}{2}\)
したがって解は
\(z=\sqrt{2}\left\{\cos(\displaystyle\frac{π}{4}+\displaystyle\frac{kπ}{2})+i\sin(\displaystyle\frac{π}{4}+\displaystyle\frac{kπ}{2})\right\}\)
となるから、\(k=0,1,2,3\) を代入すると
\(z=\sqrt{2}(±\displaystyle\frac{1}{\sqrt{2}}±\displaystyle\frac{1}{\sqrt{2}}i)\) (複合任意)
\(z=1+i,\ -1+i,\ -1-i,\ 1-i\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→z^n=1 の解と求値問題 back→z^n=1 の解