複素数平面上のなす角の計算による求め方について見ていきます。
・複素数平面となす角(原点まわり)
複素数の商を利用すると、原点まわりのなす角を求めることができます。
\(β=r_1(\cosθ_1+i\sinθ_1)\)、\(γ=r_2(\cosθ_2+i\sinθ_2)\)
とおくと (ただし\(r_1,r_2\)はともに正) 、商\(\displaystyle\frac{γ}{β}\)は
\(\displaystyle\frac{γ}{β}=\displaystyle\frac{r_2}{r_1}\{\cos(θ_2-θ_1)+i\sin(θ_2-θ_1)\}\)
(今回はなす角について検討したいので、拡大縮小を表す大きさ\(r\)の部分についてはあまり触れないように話を進めていきます。)
ここで、
\(\displaystyle\frac{r_2}{r_1}=R\)、\(θ_2-θ_1=θ\) とおくと
\(\displaystyle\frac{γ}{β}=R(\cosθ+i\sinθ)\)
であり、\(θ_2-θ_1\) は\(B(β),C(γ)\)とおくと、\(OB\)と\(OC\)のなす角\(θ\)を表しているので次のことが成り立ちます。
\(\angleβ0γ=\arg\displaystyle\frac{γ}{β}\)・・・①
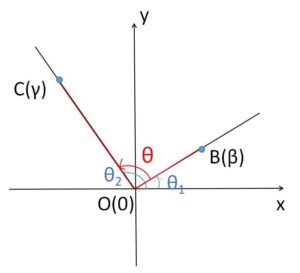
つまり、商を計算してその極形式を求めればなす角\(θ\)が分かるということですが、少し注意点があります。
まず、複素数の偏角は左周り(反時計回り)を正にとった向きのある角なので、①で求めた\(\angleβ0γ\)も向きのある角です。よって、偏角を正でとった場合には半直線\(OB\)を左周りに回転させた位置に\(OC\)が、負でとった場合には右周りに回転させた位置に\(OC\)があるということです。
また、①は\(2kπ\) (\(k\)は整数) のズレなら成り立つということを意味しています。これは \(2kπ\) のズレの違いだけなら位置関係が変わらないからですが、偏角\(θ\)を \(-π<θ≦π\) のように限定しても問題ないです。
また向きを気にしない角 \(\angle BOC\) (\(0\)以上\(π\)以下) を求めるには図で判断するか、もしくは求めた極形式の偏角を \(-π<θ≦π\) の範囲でとって絶対値をつければ機械的に処理することができます。
なおベクトルと対応させると、\(β\)は\(\overrightarrow{OB}\)を表す複素数、\(γ\)は\(\overrightarrow{OC}\)を表す複素数で
\(γ=R(\cosθ+i\sinθ)\cdotβ\)
より、\(\displaystyle\frac{γ}{β}=R(\cosθ+i\sinθ)\) は、\(\overrightarrow{OB}\)を\(θ\)回転させて\(R\)倍すると\(\overrightarrow{OC}\)になるということを意味しています。
・複素数平面となす角(ある点まわり)
\(A(α),B(β),C(γ)\) とおくとき、\(α\)まわりの角 \(\angleβαγ\) は上記原点まわりの角に帰着させて求めることが可能です。
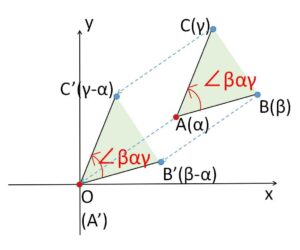
つまり、全体を\(-α\)だけ平行移動させると移動後の点はそれぞれ \(A'(0),B'(β-α),C'(γ-α)\) となるので
\(\angle βαγ=\arg\displaystyle\frac{γ-α}{β-α}\)
です。もちろんこれも\(AB\)から見た向きのある角です。
ベクトルで考えると
\(\displaystyle\frac{γ-α}{β-α}=R(\cosθ+i\sinθ)\)
(\(γ-α=R(\cosθ+i\sinθ)(β-α)\))
で表されるとき、\(\overrightarrow{AB}\) を\(A\)まわりに\(θ\)だけ回転させて\(R\)倍すると\(\overrightarrow{AC}\) となることを意味しています。
(例題)
\(α=2+2i\)、\(β=3+4i\)、\(γ=5+3i\) を表す点をそれぞれ\(A,B,C\)とするとき、\(\angle BAC\) (\(0°\)以上\(180°\)以下) の大きさを求めよ。
(解答)
\(\displaystyle\frac{γ-α}{β-α}\)
\(=\displaystyle\frac{(5+3i)-(2+2i)}{(3+4i)-(2+2i)}\)
\(=\displaystyle\frac{3+i}{1+2i}\)
\(=\displaystyle\frac{(3+i)(1-2i)}{(1+2i)(1-2i)}\) (分母の実数化)
\(=\displaystyle\frac{5-5i}{5}\)
\(=1-i\)
\(=\sqrt{2}\{\cos(-\displaystyle\frac{π}{4})+i\sin(-\displaystyle\frac{π}{4})\}\)
よって、\(\angle BAC=45°\)
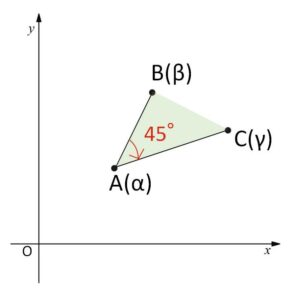
上記のように偏角を負でとると、\(\overrightarrow{AB}\) を右回り(時計回り)に \(45°\) 回転させて \(\sqrt{2}\) 倍すると、\(\overrightarrow{AC}\) になることが分かる。
\(\cos(-\displaystyle\frac{π}{4})+i\sin(-\displaystyle\frac{π}{4})=\cos\displaystyle\frac{7π}{4}+i\sin\displaystyle\frac{7π}{4}\)
とすれば、\(\overrightarrow{AB}\) を左回り(反時計回り)に \(315°\) 回転させて \(\sqrt{2}\) 倍すると、\(\overrightarrow{AC}\) になると見ることもできる。いずれにせよ \(\angle BAC=45°\) である。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平行(共線)・垂直条件 back→分点と重心