平行移動や回転移動を利用した軌跡・領域の例題です。
(例題1)
複素数\(z\)は、複素数平面上で点\(1\)を中心とする半径\(1\)の円周上を動く。このとき
\(w=iz+i\)
で表される点\(w\)の軌跡を求めよ。
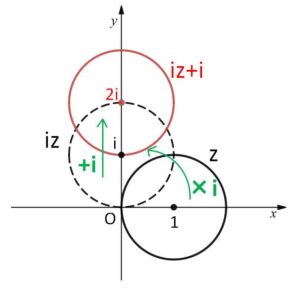
まず\(iz\)ですが、これは反時計回りに\(\displaystyle\frac{π}{2}\)の回転移動(拡大縮小なし)で、さらに\(+i\)は虚軸方向に\(+1\)の平行移動です。\(w=iz+i\) はこの2つの移動の組み合わせです。
(解答)
\(w=iz+i\) について
\(iz\)は原点を中心とする\(+\displaystyle\frac{π}{2}\)の回転移動、\(+i\)は虚軸方向に\(+1\)する平行移動。
よって、\(z\)は中心が点\(1\)の半径\(1\)の円周上を動くことから、\(w=iz+i\) の軌跡は
点\(2i\)を中心とする半径\(1\)の円周
となる。
(参考)
\(w=i(z+1)\) として、初めに実軸方向に\(+1\)だけ平行移動して、その後\(+\displaystyle\frac{π}{2}\)の回転移動をすると考えてもよい。
(例題2)
複素数平面上で、複素数\(α\)は2点 \(1+i,\ 1-i\) を結ぶ線分上を動き、複素数\(β\)は原点を中心とする半径\(1\)の円周上を動くものとする。
(1)\(α+β\)が複素数平面上を動く範囲の面積を求めよ。
(2)\(αβ\)が複素数平面上を動く範囲の面積を求めよ。
今回は動く点が2種類(変数が2つ)になっていますが、2動点(2変数)の場合は1つを固定するのが基本です。
なお、数式のみで解くこともできます(参考参照)。
(解答)
(1)
まず\(α\)を固定する。
\(β+α\) は\(β\)を\(+α\)の分だけ平行移動していることになるので、\(β+α\)は\(α\)(実部は\(1\)で固定)を中心とする半径\(1\)の円周上を表す。
\(α\)を動かすと、この円が虚軸方向に動くことになるので、\(α\)の虚部の最大値と最小値が\(1,-1\)であるから、\(α+β\)の動く範囲は下図の通り。
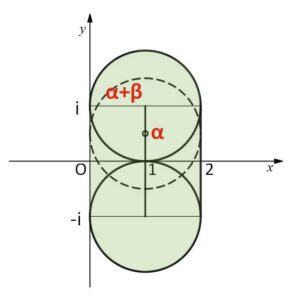
よって面積\(S_1\)は、円と長方形を組み合わせて
\(S_1=π\cdot1^2+2\cdot2=\)\(π+4\)
(2)
\(β\)を固定する。
\(|β|=1\)より、\(αβ\)は\(1+i,1-i\) を結ぶ線分を原点周りに\(\argβ\)だけ回転したものを表す。
\(β\)を動かすと、線分が原点を中心として1回転することになる。
回転移動前の \(1+i,1-i\) を結ぶ線分上の点で、原点から最も近い場所との距離は\(1\)、遠い場所との距離は \(\sqrt{1^2+1^2}=\sqrt{2}\) だから、\(αβ\)の動く範囲は原点を中心とする半径\(1\)の円と半径\(\sqrt{2}\)の円の間の部分となる。
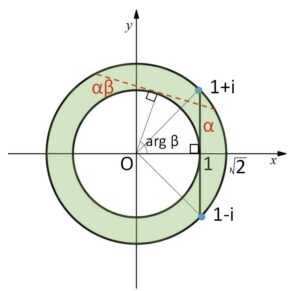
よって面積\(S_2\)は
\(S_2=π\cdot(\sqrt{2})^2-π\cdot1^2=\)\(π\)
(参考)
\(α=1+ti\) (\(-1≦t≦1\))
\(β=\cosθ+i\sinθ\) (\(0≦θ<2π\))
とおける。
(1)
\(α+β=(1+\cosθ)+(t+\sinθ)i\)
\(α+β=x+yi\) とおくと
\(x=1+\cosθ\)、\(y=t+\sinθ\)
つまり
\(x-1=\cosθ\)、\(y-t=\sinθ\)
だから、\(α+β\)の動く部分は
\((x-1)^2+(y-t)^2=1\) (\(-1≦t≦1\))
で表される領域である。\(t\)を動かすと\(y\)軸方向に半径\(1\)の円が平行移動するので、上記と同じ領域が得られる。
(2)
\(αβ=(1+ti)(\cosθ+i\sinθ)\)
\(=(\cosθ-t\sinθ)+(\sinθ+t\cosθ)i\)
\(αβ=x+yi\) とおくと
\(x=\cosθ-t\sinθ\)、\(y=\sinθ+t\cosθ\)
2乗和をとることで(\(θ\)を消去するイメージ)
\(x^2+y^2=1+t^2\) (\(-1≦t≦1\))
となり、この方程式が表す領域が\(αβ\)の動く範囲である。
中心は原点で固定で、\(1≦1+t^2≦2\) より、半径は\(1\)から\(\sqrt{2}\)まで変化するので、上記と同じ円をくり抜いた領域が得られる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→なす角と軌跡・領域 back→線分上を動く点と軌跡・領域