なす角と軌跡・領域の例題です。
複素数の商や極形式がポイントになります。
(例題1)
\(z\)を複素数とする。複素数平面上の3点 \(A(1),B(z),C(z^2)\) が鋭角三角形をなすような\(z\)の範囲を求め、図示せよ。
(解答)
\(A(1),B(z),C(z^2)\) のうち一致するものがあるとき
\(1=z\)、\(1=z^2\)、\(z=z^2\)
よって
\(z=1\)、\(z=±1\)、\(z(z-1)=0\) より
\(z=0,±1\) のとき三角形が作られないので
\(z≠0,±1\)
また\(A,B,C\)が一直線上にあるとき
\(z^2-z=k(z-1)\)
となる実数\(k\)が存在し
\(z(z-1)=k(z-1)\)
\(z≠1\) より \(z\)は実数。よって\(z\)が実数のとき三角形が作られないので
\(z\)は実数ではない。
ゆえに以下\(z\)は実数でないものとして進める。
(i)角\(A\)について
\(0°≦\angle A<90°\) だから
\(\displaystyle\frac{z^2-1}{z-1}=z+1\) の実部が正であればよい。
(\(r(\cosθ+i\sinθ) (r>0)\) より \(r\cosθ>0\) となる)
\(0°\)を含めたのは実部正という統一された条件で処理するためです。もちろん\(0°\)の場合は3点が一直線上にあるので三角形は作られませんが、これは最初に検討しているので問題ありません。
(ii)角\(B\)について
\(0°≦\angle B<90°\) だから
\(\displaystyle\frac{z^2-z}{1-z}=-z\) の実部が正であればよい。
(iii)角\(C\)について
\(0°≦\angle C<90°\) だから
\(\displaystyle\frac{1-z^2}{z-z^2}=\displaystyle\frac{1+z}{z}\) の実部が正であればよい。
\(z\)が実数でないとき、3点は一直線上にないので
\(\angle A,\ \angle B,\ \angle C≠0\)
以上より三角形\(ABC\)が鋭角三角形であるための条件は
\(z\)が実数ではない・・・①
\(z+1\) の実部が正・・・②
\(-z\) の実部が正・・・③
\(\displaystyle\frac{1+z}{z}\) の実部が正・・・④
\(z=x+yi\) とおくと②③④はそれぞれ
②について
\(z+1=(x+1)+yi\) より
\(x+1>0\)
つまり \(x>-1\)・・・②’
③について
\(-z=-x-yi\) より
\(-x>0\)
つまり \(x<0\)・・・③’
④について
\(\displaystyle\frac{1}{z}+1=\displaystyle\frac{1}{x+yi}+1\)
\(=\displaystyle\frac{x-yi}{x^2+y^2}+1\)
\(=\displaystyle\frac{(x+x^2+y^2)-yi}{x^2+y^2}\) より
\(x^2+x+y^2>0\)
つまり
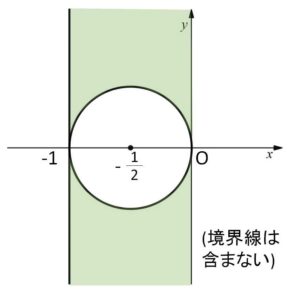
\((x+\displaystyle\frac{1}{2})^2+y^2>\displaystyle\frac{1}{4}\)・・・④’
②’③’④’の共通部分が\(z\)の動く範囲であり(\(z\)が実数でないことを満たす)、図示すると次の通り。
(例題2)
\(z\)を複素数とするとき、\(\displaystyle\frac{z-i}{z+i}\) の偏角が\(45°\)であるような\(z\)が複素数平面上で描く図形を図示せよ。
となるような正の数\(r\)が存在すればよいことになります。\(z=x+yi\) とおいて両辺を比較すればよいでしょう。
(解答)
\(r\)を正の数とすると
\(\displaystyle\frac{z-i}{z+i}=r(\cos45°+i\sin45°)\)・・・①
\(z=x+yi\) とおくと
\(\displaystyle\frac{z-i}{z+i}=\displaystyle\frac{x+(y-1)i}{x+(y+1)i}\)
\(=\displaystyle\frac{\{x+(y-1)i\}\{x-(y+1)i\}}{x^2+(y+1)^2}\)
\(=\displaystyle\frac{(x^2+y^2-1)-2xi}{x^2+(y+1)^2}\)
よって①の両辺で実部と虚部を比べると
\(\displaystyle\frac{x^2+y^2-1}{x^2+(y+1)^2}=\displaystyle\frac{r}{\sqrt{2}}\)・・・②
\(\displaystyle\frac{-2x}{x^2+(y+1)^2}=\displaystyle\frac{r}{\sqrt{2}}\)・・・③
②③より\(r\)を消去すると
\(x^2+y^2-1=-2x\)
整理すると
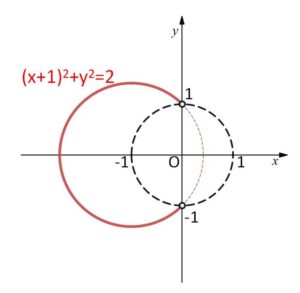
\((x+1)^2+y^2=2\)・・・④
また \(r>0\) だから②③より
\(x^2+y^2-1>0\)
\(-2x>0\)
つまり
\(x^2+y^2>1\)・・・⑤
\(x<0\)・・・⑥
④⑤⑥の共通部分が\(z\)が描く図形で、図示すると次の通り。
(注)
\(r>0\) についてですが、②③の片方だけ調べてもよいです。例えば③だけだと \(x<0\) になりますが、このとき\(r\)は正の数としてとれるので、②は調べなくても大丈夫です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→複素数平面の軌跡・領域の図形的解法