\(x^4+3x^3-3x^2-7x+6\) のような高次式の因数分解を、因数定理を利用して解く方法について見ていきます。
・高次式の因数分解
整式\(P(x)\)を因数分解するとき、\(P(k)=0\)となる\(k\)を見つけることができれば、因数定理より\(P(x)\)が\(x-k\)を因数にもつので、\(P(x)=(x-k)Q(x)\)と因数でくくり出すことができます。次に\(Q(k’)=0\)となる\(k’\)を見つけ・・・と繰り返すことで、\(P(x)\)を因数分解することができます。
今回主に学んでいくことは
①\(P(k)=0\)となる\(k\)の見つけ方
②\(Q(x)\)を求める簡単な方法(組立除法)
についてです。順番的には逆になりますがまず②について見ていきます。
・組立除法
整式\(P(x)\)を1次式\(x-k\)で割ったときの、商\(Q(x)\)と余り\(R\)を求める簡単な方法があり、これを組立除法(くみたてじょほう)とよびます。
\(P(x)=ax^3+bx^2+cx+d\) (3次式)として、\(x-k\)で割ったときの商\(Q(x)\)と余り\(R\)について考えます。
\(Q(x)\)は2次式となるので、\(Q(x)=lx^2+mx+n\)とすると
\(ax^3+bx^2+cx+d=(x-k)(lx^2+mx+n)+R\)
が成り立ち、右辺を展開して整理すると
\(ax^3+bx^2+cx+d\)
\(=lx^3+(-lk+m)x^2+(-mk+n)x\)\(+(-nk+R)\)
となり、両辺の係数を比較して、変形すると
\(l=a\), \(m=b+lk\), \(n=c+mk\), \(R=d+nk\)・・・(A)
(A)より以下のように計算することで、商の係数\(l,m,n\)と余り\(R\)が求まります。
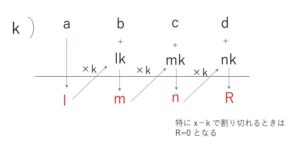
また、3次に限らず一般の整式\(P(x)\)についても同様のことが成り立ちます。
(例題1)
組立除法を用いて、次の割り算の商と余りを求めよ。
(1)\((x^3-10x+2)÷(x+2)\)
(2)\((3x^3-2x^2+4x-3)÷(3x-2)\)
(解答)
(1)
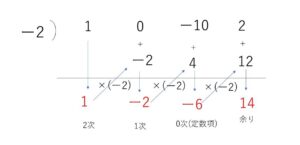
よって
\(x^3-10x+2=(x+2)(x^2-2x-6)+14\) だから
商 \(x^2-2x-6\) 余り \(14\)
(2)
\(3x^3-2x^2+4x-3=(3x-2)Q(x)+R\)\(=(x-\displaystyle\frac{2}{3})・3Q(x)+R\)
なので、\(k=\displaystyle\frac{2}{3}\)として組立除法を使います。
なお計算して得られる商は\(Q(x)\)そのものではなく、\(3Q(x)\)です。
\(x-\displaystyle\frac{2}{3}\) で割った余りを求めると
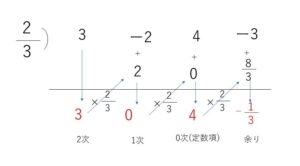
よって
\(3x^3-2x^2+4x-3\)\(=(x-\displaystyle\frac{2}{3})(3x^2+4)-\displaystyle\frac{1}{3}\) より
\(3x^3-2x^2+4x-3\)\(=(3x-2)(x^2+\displaystyle\frac{4}{3})\)\(-\displaystyle\frac{1}{3}\)
商 \(x^2+\displaystyle\frac{4}{3}\) 余り \(-\displaystyle\frac{1}{3}\)
・\(P(k)=0\) をみたす\(k\)の見つけ方
\(P(x)=ax^3+bx^2+cx+d\) とする。(ただし\(a,b,c,d\)は整数)
ここで、\(P(\displaystyle\frac{q}{p})=0\) (\(p,q\)は互いに素である整数) が存在する場合・・・(注1)、(つまり有理数\(\displaystyle\frac{q}{p}\)が\(P(x)=0\)の解であるとき) \(P(x)\)は\(px-q\)で割り切れるので、商を\(lx^2+mx+n\) とすると
\(ax^3+bx^2+cx+d=(px-q)(lx^2+mx+n)\) (\(l,m,m\)は整数)・・・(注2)
と表せます。両辺の\(x^3\)の項と定数項を比較すると
\(a=pl\) \(d=-qn\)
よって、\(p\)は\(a\)の約数、\(q\)は\(d\)の約数なので
\(\displaystyle\frac{q}{p}=±\displaystyle\frac{dの約数}{aの約数}\)・・・(B)
\(\displaystyle\frac{q}{p}\)は、\(P(\displaystyle\frac{q}{p})=0\)を満たす有理数で、これを見つけるには(B)より「定数項の約数÷最高次の係数の約数」を考えればよいことになります。
特に、最高次の係数が\(1\)のとき\(a=1\)なので、\(d\)の約数を考えることになります。
一般の整式\(P(x)\)においても同様です。
\(±\displaystyle\frac{定数項の約数}{最高次の係数の約数}\)
を考えればよい。
(注1)について
\(P(x)=0\)を満たす有理数解が存在すると仮定した場合の話なので、もちろん有理数解が存在しないケースもあります。そのときは無理数の解や虚数解をもったりします。
(注2)について
\(a,b,c,d\)が整数, \(p,q\)が互いに素である整数のとき、\(l,m,n\)が整数になるのは、「整数係数の整式が、有理数係数の整式に因数分解できるならば、整数係数でも因数分解できる」という定理(ガウスの定理)より導かれます。
まず\(l,m,n\)が有理数なのは両辺を比較すれば分かり、\(p,q\)が互いに素であることから、\(px-q\)は整数(定数)でくくり出すことができないため、\(lx^2+mx+n\)に掛ける整数がないので、係数\(l,m,n\)はすべて整数となります。
(例題2)
次の式を因数分解せよ。
(1)\(x^4+3x^3-3x^2-7x+6\)
(2)\(4x^4+8x^3+7x^2-2x-2\)
(1)
与式を\(P(x)\)とおくと、\(P(1)=1+3-3-7+6=0\) だから
\(x-1\)を因数にもつ。よって
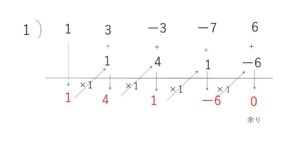
\(P(x)=(x-1)(x^3+4x^2+x-6)\)
また、\(Q(x)=x^3+4x^2+x-6\) とおくと、\(Q(1)=1+4+1-6=0\)
よって
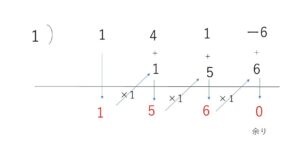
\(P(x)=(x-1)^2(x^2+5x+6)\)
\(=\)\((x-1)^2(x+2)(x+3)\)
(2)
\(±\displaystyle\frac{1,2}{1,2,4}\) です。
\(P(x)=4x^4+8x^3+7x^2-2x-2\) とおくと、
\(P(\displaystyle\frac{1}{2})\)\(=\displaystyle\frac{1}{4}+1+\displaystyle\frac{7}{4}-1-2\)\(=0\) なので、\(x-\displaystyle\frac{1}{2}\) を因数にもつ。よって
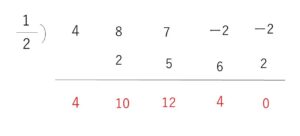
\(P(x)=\)\((x-\displaystyle\frac{1}{2})\)\((4x^3+10x^2+12x+4)\)
\(=(2x-1)(2x^3+5x^2+6x+2)\)
また、\(Q(x)=2x^3+5x^2+6x+2\) とおくと
\(Q(-\displaystyle\frac{1}{2})=-\displaystyle\frac{1}{4}+\displaystyle\frac{5}{4}-3+2\)\(=0\) なので、\(Q(x)\)は \(x+\displaystyle\frac{1}{2}\) を因数にもつから
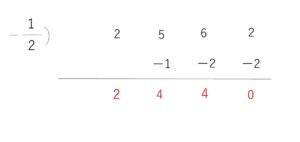
\(Q(x)=(2x-1)(x+\displaystyle\frac{1}{2})\)\((2x^2+4x+4)\)
\(=\)\((2x-1)(2x+1)(x^2+2x+2)\)
以上になります。お疲れ様でした。
ここまで見ただきありがとうございました。