絶対値を含んだ不等式の証明問題について見ていきます。
その前に絶対値の定義や、性質について見ていきます。
・絶対値の定義・性質
実数\(a\)について、数直線上で原点\(O\)から座標が\(a\)である点\(A\)までの距離を\(a\)の絶対値といい、\(|a|\)で表します。\(a\)の正負で場合分けすると次のように定義されます。
\(a≧0\)のとき、\(|a|=a\), \(a<0\)のとき、\(|a|=\)\(-\)\(a\)
距離なので、座標が負の値の場合には記号外す際にマイナスがつきます。
また絶対値について以下の性質が成り立ちます。
②\(|a|=|-a|\) (原点から\(a\),\(-a\)までの距離は同じ)
③\(|a|≧a\), \(|a|≧-a\) (絶対値をつけた\(|a|\)は、つけない\(a,-a\)と同じか、それより大きい)
④\(|a|^2=|a^2|=a^2\) (2乗の性質)
⑤\(|a||b|=|ab|\), \(b≠0\)のとき \(\displaystyle\frac{|a|}{|b|}\)\(=|\displaystyle\frac{a}{b}|\) (くっつけたり分けたりできる)
すべて、\(a≧0\), \(a<0\);\(b≧0\), \(b<0\) で場合分けすることで証明できます。
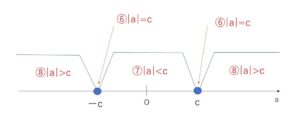
⑥\(|a|=c\) \(\leftrightarrow\) \(a=±c\)
⑦\(|a|<c\) \(\leftrightarrow\) \(-c<a<c\)
(\(|a|≦c\) \(\leftrightarrow\) \(-c≦a≦c\))
⑧\(|a|>c\) \(\leftrightarrow\) \(a<-c\) または \(a>c\)
(\(|a|≧c\) \(\leftrightarrow\) \(a≦-c\) または \(a≧c\))
数直線を考えると明らかです。
なお⑥~⑧は、\(c=0\)のときも成り立ちます。
⑥は「\(|a|=0\) \(\leftrightarrow\) \(a=±0\)」
⑦は「\(|a|<0\) \(\leftrightarrow\) \(-0<a<0\)」(\(a\)は存在しない)
⑧は「\(|a|>0\) \(\leftrightarrow\) \(a<0\) または \(a>0\)」(\(a\)は\(0\)以外のすべての実数)
(例題1)次の不等式を証明せよ。
(1)\(|a+b|≦|a|+|b|\)
(2)\(|a|-|b|≦|a+b|\)
(解答)
(1)
\((|a|+|b|)^2-|a+b|^2\)
\(=(|a|+|b|)(|a|+|b|)-(a+b)^2\)
\(=|a|^2+2|a||b|+|b|^2-(a+b)^2\)
\(=a^2+2|ab|+b^2-(a^2+2ab+b^2)\)
\(=2(|ab|-ab)\)\(≧0\) (\(|ab|≧ab\)は上記性質③より)
よって、\(|a+b|^2≦(|a|+|b|)^2\) であり
\(|a+b|≧0\), \(|a|+|b|≧0\) だから
\(|a+b|≦|a|+|b|\)
等号成立は \(|ab|=ab\) のとき、つまり\(ab≧0\) のとき
(別解)
\(-|a|≦a≦|a|\)・・・(A), \(-|b|≦b≦|b|\)・・・(B)より、辺々足すと
\(-(|a|+|b|)≦a+b≦|a|+|b|\)
よって、\(|a+b|≦|a|+|b|\) (上記性質⑦より)
等号成立は、(A)(B)の左側両方 または 右側両方の等号が成立するときなので
\(a≦0\)かつ\(b≦0\) または \(a≧0\) かつ \(b≧0\)
(2)
(1)の不等式で、\(a\)のかわりに\(a+b\)、\(b\)のかわりに\(-b\)とおくと
\(|(a+b)-b|≦|a+b|+|-b|\)
よって、\(|a|≦|a+b|+|b|\) であるから
\(|a|-|b|≦|a+b|\)
等号成立は、(1)での\(ab≧0\)の\(a\)を\(a+b\)、\(b\)を\(-b\)とすればよいので
\((a+b)(-b)≧0\) つまり \(b(a+b)≦0\) のとき。
(別解)2乗をとる方法
(ア)\(|a|-|b|<0\)のときは、明らかに成り立つ。
(イ)\(|a|-|b|≧0\) のとき
\(|a+b|^2-(|a|-|b|)^2\)
\(=a^2+2ab+b^2-(|a|^2-2|a||b|+|b|^2)\)
\(=a^2+2ab+b^2-(a^2-2|ab|+b^2)\)
\(=2(|ab|+ab)\)\(≧0\) (性質③より)
よって、\((|a|-|b|)^2≦|a+b|^2\)であり
\(|a|-|b|≧0\), \(|a+b|≧0\) だから
\(|a|-|b|≦|a+b|\)
等号は、\(|a|-|b|≧0\) かつ \(|ab|=-ab\) のときであり
\(|a|≧|b|\) かつ \(ab≦0\) のとき。
\(|a|-|b|≦|a+b|≦|a|+|b|\) (三角不等式)
となります。これは覚えてしまってもよいです。
(例題2)
\(|x|<1\), \(|y|<1\) のとき、次の不等式を証明せよ。
\(|\displaystyle\frac{x+y}{1+xy}|<1\)
(解答1)2乗する方法
\(|\displaystyle\frac{x+y}{1+xy}|<1\) \(\leftrightarrow\) \(|x+y|<|1+xy|\) なので、\(|x+y|<|1+xy|\)を証明すればよい。
\(|1+xy|^2-|x+y|^2\)
\(=(1+xy)^2-(x+y)^2\)
\(=(x^2y^2+2xy+1)-(x^2+2xy+y^2)\)
\(=x^2y^2-x^2-y^2+1\)
\(=(x^2-1)(y^2-1)\)
ここで、\(|x|<1\), \(|y|<1\) より、\(x^2<1\), \(y^2<1\) だから
\((x^2-1)(y^2-1)>0\)
よって、\(|x+y|^2<|1+xy|^2\)
\(|x+y|≧0\),\(|1+xy|≧0\) より
\(|x+y|<|1+xy|\)
以上から \(|\displaystyle\frac{x+y}{1+xy}|<1\) である。
(解答2)証明したい不等式の絶対値を外す変形をする方法
\(-1<\displaystyle\frac{x+y}{1+xy}<1\) を示すことを考える。
\(1-\displaystyle\frac{x+y}{1+xy}\)
\(=\displaystyle\frac{xy+1-x-y}{1+xy}\)
\(=\displaystyle\frac{(x-1)(y-1)}{1+xy}\)・・・(i)
ここで、\(|x|<1\), \(|y|<1\) より、\(x<1\),\(y<1\)。
また、\(|xy|<1\)だから \(-1<xy\)
ゆえに、\((x-1)(y-1)>0\), \(1+xy>0\) であるから (i)\(>0\)
よって、\(\displaystyle\frac{x+y}{1+xy}<1\)
次に
\(\displaystyle\frac{x+y}{1+xy}-(-1)\)
\(=\displaystyle\frac{x+y+xy+1}{1+xy}\)
\(=\displaystyle\frac{(x+1)(y+1)}{1+xy}\)・・・(ii)
ここで、\(|x|<1\), \(|y|<1\) より、\(-1<x\), \(-1<y\)。
ゆえに、\((x+1)(y+1)>0\), \(1+xy>0\) であるから (ii)\(>0\)
よって、\(-1<\displaystyle\frac{x+y}{1+xy}\)
以上から、\(-1<\displaystyle\frac{x+y}{1+xy}<1\)
したがって、\(|\displaystyle\frac{x+y}{1+xy}|<1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ back→大小比較