ベクトルの演算と図示②

引き続き基礎的な演習です。今回は図形の色が濃い問題です。

(例題1)
正六角形\(ABCDEF\)において \(\overrightarrow{AB}=\vec{a}\),　\(\overrightarrow{AF}=\vec{b}\) とし、線分\(AD\) と 線分\(BE\) の交点を\(O\)とする。また、線分\(OC\)の中点を\(G\)、線分\(OE\)の中点を\(H\)とする。

(1)\(\overrightarrow{BC}\), \(\overrightarrow{AC}\), \(\overrightarrow{AD}\), \(\overrightarrow{CE}\) を \(\vec{a},\vec{b}\) を用いて表せ。
(2)\(\overrightarrow{GH}\) を \(\vec{a},\vec{b}\) を用いて表せ。

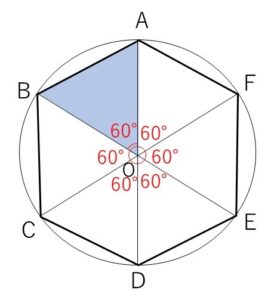
解答に入る前に正六角形についてざっくりと説明します。
まず正六角形は円周を6等分する点を結ぶことにより円に内接させることができます(弧に対する中心角がすべて等しいので弦も等しくなる)。
円の中心を\(O\)として\(O\)と正六角形の各頂点を結ぶと6つの三角形ができますが、これらは三辺相等(2辺は円の半径、1辺は正六角形の一辺)により全て合同です。そしてこの三角形は2辺が円の半径なので二等辺三角形で、さらに1つの角が60°だから正三角形となります。
また 60°×3=180° なので、\(AOD\)は一直線 (他の\(BOE\),\(COF\)も同様に一直線) となっているため、線分\(AD\),\(BE\),\(CF\) は点\(O\)で交わることになります。

(解答)
(1)

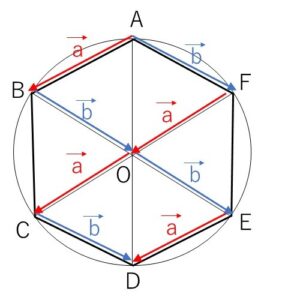
図より
\(\overrightarrow{BC}\)
\(=\overrightarrow{BO}+\overrightarrow{OC}\)
\(=\vec{b}+\vec{a}\)
\(=\vec{a}+\vec{b}\)

\(\overrightarrow{AC}\)
\(=\overrightarrow{AB}+\overrightarrow{BC}\)
\(=\vec{a}+(\vec{a}+\vec{b})\)
\(=2\vec{a}+\vec{b}\)

\(\overrightarrow{AD}\)
\(=\overrightarrow{AO}+\overrightarrow{OD}\)
\(=2(\vec{a}+\vec{b})\)
\(=2\vec{a}+2\vec{b}\)

\(\overrightarrow{CE}\)
\(=\overrightarrow{CD}+\overrightarrow{DE}\)
\(=\vec{b}-\vec{a}\)
\(=-\vec{a}+\vec{b}\)

(2)

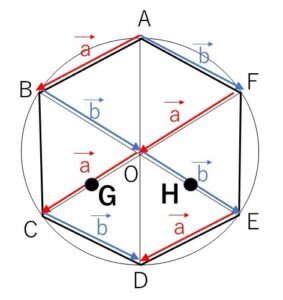
\(\overrightarrow{GH}\)
\(=\overrightarrow{GO}+\overrightarrow{OH}\)
\(=-\displaystyle\frac{1}{2}\vec{a}+\displaystyle\frac{1}{2}\vec{b}\)

(例題2)
平行四辺形\(ABCD\)において、対角線の交点を\(E\)、辺\(BC\)を\(2:1\)の比に内分する点を\(F\)とする。\(\overrightarrow{AB}=\vec{b}\),　\(\overrightarrow{AD}=\vec{d}\),　\(\overrightarrow{AE}=\vec{e}\),　\(\overrightarrow{AF}=\vec{f}\) とするとき

(1)\(\vec{e},\vec{f}\) を \(\vec{b},\vec{d}\) を用いて表せ。
(2)\(\vec{b},\vec{d}\) を \(\vec{e},\vec{f}\) を用いて表せ。

(1)

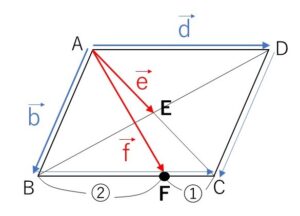
\(\vec{e}\)\(=\displaystyle\frac{1}{2}\overrightarrow{AC}\)
\(=\displaystyle\frac{1}{2}(\vec{b}+\vec{d})\)
\(=\displaystyle\frac{1}{2}\vec{b}+\displaystyle\frac{1}{2}\vec{d}\)

\(\vec{f}\)\(=\overrightarrow{AB}+\overrightarrow{BF}\)
\(=\overrightarrow{AB}+\displaystyle\frac{2}{3}\overrightarrow{BC}\)
\(=\vec{b}+\displaystyle\frac{2}{3}\vec{d}\)

(2)

(1)より
\(\displaystyle\frac{1}{2}\vec{b}+\displaystyle\frac{1}{2}\vec{d}=\vec{e}\)・・・①
\(\vec{b}+\displaystyle\frac{2}{3}\vec{d}=\vec{f}\)・・・②

①×2－② より \(\vec{b}\)を消去して
\(\displaystyle\frac{1}{3}\vec{d}=2\vec{e}-\vec{f}\)
よって
\(\vec{d}=6\vec{e}-3\vec{f}\)

①より
\(\vec{b}=2\vec{e}-\vec{d}\) だから
\(\vec{b}=2\vec{e}-(6\vec{e}-3\vec{f})\)
よって
\(\vec{b}=-4\vec{e}+3\vec{f}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの成分と大きさ①　back→ベクトルの演算と図示①