ベクトルの成分と大きさ①

ベクトルの成分表示について見ていきます。

・ベクトルの成分

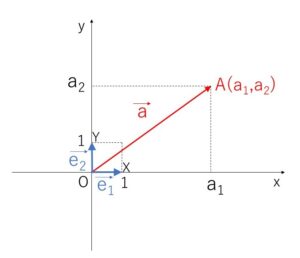
平面ベクトルを座標平面におくことで、ベクトルを「横方向,縦方向」に幾らか動いたものとして表現することができます。

原点が\(O\)の座標平面上において、あるベクトル\(\vec{a}\)に対して\(\vec{a}=\overrightarrow{OA}\)となる点\(A(a_1,a_2)\)をとります。

ここで、\(x\)軸,\(y\)軸の正の向きと同じ向きの単位ベクトルを基本ベクトルといい、\(\vec{e_1},\vec{e_2}\) で表します。つまり\(X(1,0)\),\(Y(0,1)\)とすると、\(\vec{e_1}=\overrightarrow{OX}\), \(\vec{e_2}=\overrightarrow{OY}\) となります。

すると、\(\vec{a}\)を基本ベクトルを用いて次のように表すことができ、これを\(\vec{a}\)の基本ベクトルによる表示といいます。

\(\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}\)

また、\(a_1,a_2\) をそれぞれ\(\vec{a}\)の\(x\)成分,\(y\)成分といい\(\vec{a}\)を次のように表示することもでき、これを\(\vec{a}\)の成分表示といいます。

\(\vec{a}=(a_1,a_2)\)

特徴的なベクトルの成分表示は次の通りです。
\(\vec{0}=(0,0)\),　\(\vec{e_1}=(1,0)\),　\(\vec{e_2}=(0,1)\)

ところで、2つのベクトルが等しくなることは、原点を始点に考えると終点が一致すればよいことから、2つのベクトルの\(x,y\)成分が等しくなることなので、\(\vec{b}=(b_1,b_2)\) とすると

\(\vec{a}=\vec{b}\)　\(⇔\)　\(a_1=b_1\) かつ　\(a_2=b_2\)

が成り立ちます。

そして、\(\vec{a}\) の大きさについては原点と\((a_1,a_2)\)の距離を考えると

\(|\vec{a}|=\sqrt{a_1^2+a_2^2}\)

となります。

・成分表示による演算
ベクトルの成分表示による演算は次の通りです。

(解説)
和・差については横縦の方向の移動、実数倍については相似な図形を考えればほとんど自明ですが、丁寧に示すと次の通りです。

\(\vec{a}=(a_1,a_2)\),　\(\vec{b}=(b_1,b_2)\) として、基本ベクトルを \(\vec{e_1},\vec{e_2}\) とする。

(1)
\((a_1,a_2)+(b_1,b_2)\)
\(=(a_1\vec{e_1}+a_2\vec{e_2})+(b_1\vec{e_1}+b_2\vec{e_2})\)
\(=(a_1+b_1)\vec{e_1}+(a_2+b_2)\vec{e_2}\)
\(=(a_1+b_1,a_2+b_2)\)

(差についても同様に示せる)

(2)
\(k(a_1,a_2)\)
\(=k(a_1\vec{e_1}+a_2\vec{e_2})\)
\(=ka_1\vec{e_1}+ka_2\vec{e_2}\)
\(=(ka_1,ka_2)\)

(3)については(2)→(1)と組み合わせると示せる。

・2点間のベクトル

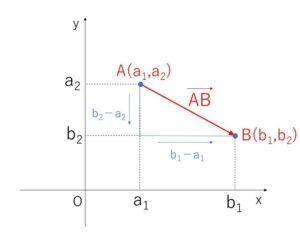
2点 \(A(a_1,a_2)\), \(B(b_1,b_2)\) とすると、\(\overrightarrow{AB}\) の成分と大きさは次の通りです。

\(\overrightarrow{AB}\)
\(=\overrightarrow{OB}-\overrightarrow{OA}\)
\(=(b_1,b_2)-(a_1,a_2)\)
\(=(b_1-a_1,b_2-a_2)\)

(横縦方向の移動を考えても成り立つことが分かる)

\(|\overrightarrow{AB}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}\)

(2点間の距離になる)

簡単な例題をやって終わりにしましょう。本格的な例題については次回にします。

(例題)
\(\vec{a}=(1,-2)\), \(\vec{b}=(0,3)\), \(\vec{c}=(4,-3)\) のとき、
ベクトル \(2\vec{a}-3\vec{b}+\vec{c}\) の成分とその大きさを求めよ。

(解答)
\(2\vec{a}-3\vec{b}+\vec{c}\)
\(=2(1,-2)-3(0,3)+(4,-3)\)
\(=(2,-4)+(0,-9)+(4,-3)\)
\(=(2+0+4,-4-9-3)\)
\(=(6,-16)\)

よって
\(|2\vec{a}-3\vec{b}+\vec{c}|\)
\(=\sqrt{6^2+(-16)^2}\)
\(=2\sqrt{73}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの成分と大きさ②　back→ベクトルの演算と図示②