ベクトルの成分と大きさに関する演習です。
(例題1)
(1)\(\vec{a}=(24,35)\), \(\vec{b}=(31,44)\) とする。
\(4\vec{x}+3\vec{y}=\vec{a}\), \(5\vec{x}+4\vec{y}=\vec{b}\) を満たす\(\vec{x}\)を求めよ。
(2)\(\vec{a}=(-3,2)\), \(\vec{b}=(2,1)\) とする。\(|\vec{a}+t\vec{b}|\) を最小にする\(t\)の値と、このときの最小値を求めよ。
(解答)
(1)
\(4\vec{x}+3\vec{y}=\vec{a}\)・・・①
\(5\vec{x}+4\vec{y}=\vec{b}\)・・・②
①×4-②×3 より\(\vec{y}\)を消去すると
\(\vec{x}=4\vec{a}-3\vec{b}\)
よって
\(\vec{x}=4(24,35)-3(31,44)\)
\(=(3,8)\)
(2)
\(|\vec{a}+t\vec{b}|^2\)
\(=|(-3,2)+t(2,1)|^2\)
\(=|(-3+2t,2+t)|^2\)
\(=(-3+2t)^2+(2+t)^2\)
\(=5t^2-8t+13\)
\(=5(t-\displaystyle\frac{4}{5})^2+\displaystyle\frac{49}{5}\)
\(|\vec{a}+t\vec{b}|≧0\) より
最小値は \(t=\displaystyle\frac{4}{5}\) のとき
\(\sqrt{\displaystyle\frac{49}{5}}\)\(=\displaystyle\frac{7}{\sqrt{5}}\)
(参考)図形的解釈
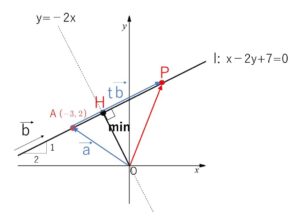
ベクトル方程式の考え方を含みますが、\(|\vec{a}+t\vec{b}|\) の図形的解釈は次の通りです。
\(\vec{a}=\overrightarrow{OA}\) とすると、\(\vec{a}+t\vec{b}\) は
「\(O→A\) の移動, \(A\)から\(\vec{b}\)の方向に移動」のベクトル
となっているので、\(\overrightarrow{OP}=\vec{a}+t\vec{b}\) とおくと、点\(P\)は点\(A\)を通り、\(\vec{b}\)に平行な直線\(l\)上の点になっています。
よって\(|\vec{a}+t\vec{b}|\) は原点と直線\(l\)上の点との距離を表しているので、このベクトルの最小値は原点と直線の距離\(OH\)になります。
実際に計算してみると
まず直線\(l\)の方程式は、\(\vec{b}=(2,1)\) が「横に2,縦に1移動」するベクトルであることから、傾きが\(\displaystyle\frac{1}{2}\)で、点\(A(-3,2)\) を通るので
\(y=\displaystyle\frac{1}{2}(x+3)+2\)
整理すると
\(x-2y+7=0\)・・・(i)
したがって最小値は
\(\displaystyle\frac{|7|}{\sqrt{1^2+(-2)^2}}\)\(=\displaystyle\frac{7}{\sqrt{5}}\)
また、そのときの点\(P\)の座標(垂線の足\(H\)になる)は(i)と、(i)に垂直な原点を通る直線
\(y=-2x\)・・・(ii)
の交点になるので (i)(ii)よりその座標は
\(H(-\displaystyle\frac{7}{5},\displaystyle\frac{14}{5})\)
\(\vec{a}+t\vec{b}=(-3+2t,2+t)\) だから
\(-3+2t=-\displaystyle\frac{7}{5}\) かつ \(2+t=\displaystyle\frac{14}{5}\) より
\(t=\displaystyle\frac{4}{5}\)
となります。
(例題2)
ベクトル\(\vec{a}=(1,-1)\) に対し、\(|\vec{a}+t\vec{b}|\) は \(t=-1\) のとき最小値\(1\)をとるという。\(\vec{b}\)を求めよ。
(解答)
\(\vec{b}=(x,y)\) とおくと
\(|\vec{a}+t\vec{b}|^2\)
\(=|(1,-1)+t(x,y)|^2\)
\(=|(1+tx,-1+ty)|^2\)
\(=(1+tx)^2+(-1+ty)^2\)
(\(t\)を変化させたとき \(t=-1\) で最小値をとるので、以下\(t\)の関数としてみる)
\(=(x^2+y^2)t^2+2(x-y)t+2\)
ここで \(x^2+y^2=0\) とすると、\(x=y=0\)
このとき \(|\vec{a}+t\vec{b}|^2=2\) より \(|\vec{a}+t\vec{b}|=\sqrt{2}\) となり、最小値が\(1\)とならないので不適。
よって \(x^2+y^2≠0\) で
\(|\vec{a}+t\vec{b}|^2\)
\(=(x^2+y^2)\left(t+\displaystyle\frac{x-y}{x^2+y^2}\right)^2-\displaystyle\frac{(x-y)^2}{x^2+y^2}+2\)
\(=(x^2+y^2)\left(t+\displaystyle\frac{x-y}{x^2+y^2}\right)^2+\displaystyle\frac{2xy}{x^2+y^2}+1\)
\(|\vec{a}+t\vec{b}|≧0\) より
\(t=-1\) で \(|\vec{a}+t\vec{b}|^2\) が 最小値\(1^2\) をとる。
\(x^2+y^2>0\) より
\(-\displaystyle\frac{x-y}{x^2+y^2}=-1\)・・・①
\(\displaystyle\frac{2xy}{x^2+y^2}+1=1^2\)・・・②
②より
\(\displaystyle\frac{2xy}{x^2+y^2}=0\) だから
\(x=0\) または \(y=0\)
(ア)\(x=0\) のとき \(y≠0\) で
①より\(\displaystyle\frac{y}{y^2}=-1\)
よって \(y=-1\)
(イ)\(y=0\) のとき \(x≠0\) で
①より \(-\displaystyle\frac{x}{x^2}=-1\)
よって \(x=1\)
以上から
\(\vec{b}=\)\((0,-1)\), \((1,0)\)
(例題3)
ベクトル \((2\cosθ+3\sinθ,\cosθ+4\sinθ)\) の長さの最大値とそのときの\(θ\)の値を求めよ。ただし\(0°≦θ≦180°\) とする。
(解答)
\(|(2\cosθ+3\sinθ,\cosθ+4\sinθ)|^2\)
\(=(2\cosθ+3\sinθ)^2+(\cosθ+4\sinθ)^2\)
\(=25\sin^2θ+5\cos^2θ+20\sinθ\cosθ\)
(\(\sinθ,\cosθ\) の2次式のみで表されているので、\(2θ\)に統一します)
\(=25\cdot\displaystyle\frac{1-\cos2θ}{2}+5\cdot\displaystyle\frac{1+\cos2θ}{2}+10\sin2θ\)
\(=10(\sin2θ-\cos2θ)+15\)
(角が\(2θ\)で統一されていて、三角関数の種類が違うので合成します)
\(=10\sqrt{2}\sin(2θ-45°)+15\)
\(0°≦θ≦180°\) より
\(-45°≦2θ-45°≦315°\)
\(-1≦\sin(2θ-45°)≦1\)
よって最大値は
\(\sqrt{10\sqrt{2}+15}\)
\(=\sqrt{15+2\sqrt{50}}\)
\(=\sqrt{(\sqrt{10}+\sqrt{5})^2}\)
\(=\sqrt{10}+\sqrt{5}\)
このとき
\(2θ-45°=90°\)
\(θ=67.5°\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの平行① back→ベクトルの成分と大きさ①