今までベクトルの平行という言葉を何気なく使うこともありましたが、その定義や関係する知識について見ていきます。
・ベクトルの平行
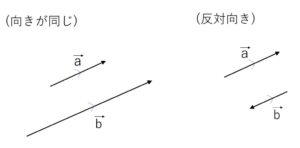
\(\vec{0}\)でない2つのベクトル\(\vec{a},\vec{b}\)の向きが同じか、反対向きであるとき、\(\vec{a}\)と\(\vec{b}\)は平行であるといい、\(\vec{a}/\!/\vec{b}\) と書きます。
ベクトルの実数倍の定義からベクトル平行の条件は次の通りです。
\(\vec{a}/\!/\vec{b}\) \(⇔\) \(\vec{a}=k\vec{b}\) となる実数\(k\)が存在する
また平面ベクトルにおいて
\(\vec{a}=(a_1,a_2)\) \(\vec{b}=(b_1,b_2)\) (\(\vec{a}≠0\),\(\vec{b}≠0\)) と成分表示されている場合は
\(\vec{a}/\!/\vec{b}\)
\(⇔\) \((a_1,a_2)=k(b_1,b_2)\) となる実数\(k\)が存在する
もしくは
となります。
①が成り立つ理由は次の通りです。
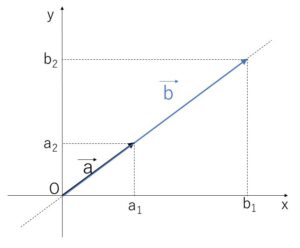
\(\vec{a}/\!/\vec{b}\) のとき
\(a_1:a_2=b_1:b_2\) が成り立つので
\(a_1b_2=a_2b_1\) より
\(a_1b_2-a_2b_1=0\)
逆に \(a_1b_2-a_2b_1=0\) のとき
\(a_1:a_2=b_1:b_2\) になるので
\(\vec{a}/\!/\vec{b}\)
問題を解く際には、\(\vec{a}≠0\), \(\vec{b}≠0\) の確認をしてください。
等式 \(a_1b_2-a_2b_1=0\) は \(\vec{a}=(a_1,a_2)=\vec{0}\) のときにも成り立ちますし、\(\vec{a}=k\vec{b}\) についても、\(\vec{a}=\vec{0}\) のとき \(k=0\)とすれば成り立ちます。
・3点が1直線上にある条件
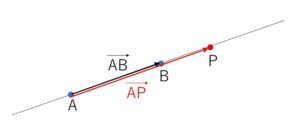
異なる2点\(A,B\)に対して、点\(P\)が直線\(AB\)上にある(\(A,B,P\)が1直線上にある)条件は、\(\overrightarrow{AB}/\!/\overrightarrow{AP}\) か\(\overrightarrow{
AP}=\vec{0}\) となるので
また、\(k\)の値に対応した点\(P\)の位置は次の通りです。
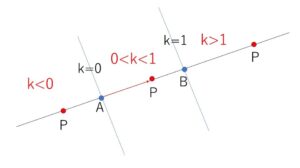
点\(A,B\)が異なる点であるという条件に注意してください。
点\(A,B\)が一致している場合には、点\(P\)はどこにあっても1直線上にありますし、
\(\overrightarrow{AP}=k\overrightarrow{AB}\) となる実数\(k\)が存在するとは限りません。(右辺が\(k\)の値によらず\(\vec{0}\)となるので、等式が成り立つのは\(P\)も\(A,B\)に一致するときのみになる)
\(\overrightarrow{AP}=(a_1,a_2)\), \(\overrightarrow{AB}=(b_1,b_2)\) とどちらも成分表示にした場合には、\(P\)が\(A\)に一致、\(A,B\)が一致の場合も含めて \(a_1b_2-a_2b_1=0\) が利用できます。(例えば\(A,B\)が一致のときは、\(b_1=b_2=0\)より任意の\(a_1,a_2\)で成り立つ)
最後に簡単な演習をして終わりにします。本格的な問題は次回に回します。
(例題)
(1)\(\vec{a}=(p,1)\), \(\vec{b}=(3,p+2)\) が平行になるように\(p\)の値を定めよ。
(2)3点 \(A(-1,-10)\), \(B(2,-a)\), \(C(a,0)\) が一直線上にあるように、定数\(a\)の値を定めよ。
(解答)
(1)
\(\vec{a},\vec{b}\) のどちらも\(\vec{0}\)でない。
\(p(p+2)-3=0\)
\(p^2+2p-3=0\)
\((p+3)(p-1)=0\)
\(p=-3,1\)
(別解)
\(\vec{a},\vec{b}\) のどちらも\(\vec{0}\)でない。
\(\vec{a}=k\vec{b}\) より
\((p,1)=(3k,k(p+2))\)
\(p=3k\)・・・①
\(1=k(p+2)\)・・・②
①を②に代入して
\(1=\displaystyle\frac{p}{3}(p+2)\)
\(3=p(p+2)\)
\(p^2+2p-3=0\) (同じ方程式が出てくる)
\(p=-3,1\) (このとき①より\(k\)は実数)
(2)
\(A(-1,-10)\), \(B(2,-a)\), \(C(a,0)\) において
\(\overrightarrow{AB}=(3,-a+10)\), \(\overrightarrow{AC}=(a+1,10)\)
\(A,B,C\)が一直線上にあるとき
\(3\cdot10-(-a+10)(a+1)=0\)
\(a^2-9a+20=0\)
\((a-4)(a-5)=0\)
\(a=4,5\)
(別解)
\(A(-1,-10)\), \(B(2,-a)\), \(C(a,0)\) において、点\(A,B\)は一致していないから
\(\overrightarrow{AC}=k\overrightarrow{AB}\) より
\((a+1,10)=k(3,-a+10)\)
\(a+1=3k\)・・・③
\(10=k(-a+10)\)・・・④
③を④に代入して
\(10=\displaystyle\frac{a+1}{3}(-a+10)\)
\(30=(a+1)(-a+10)\)
\(a^2-9a+20=0\) (同じ方程式)
\(a=4,5\) (このとき③より\(k\)は実数)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの平行② back→ベクトルの成分と大きさ②