平行四辺形に関するベクトルについて見ていきます。
・平行四辺形の成立条件
平行四辺形の成立条件は次の通りです。
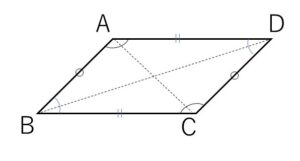
平行四辺形\(ABCD\)において
(1)2組の対辺が平行 (\(AB/\!/DC\) かつ \(AD/\!/BC\))
(2)2組の対辺が等しい (\(AB=DC\) かつ \(AD=BC\))
(3)2組の対角が等しい (\(\angle A=\angle C\) かつ \(\angle B=\angle D\))
(4)1組の対辺が平行かつ等しい
(5)対角線が互いに他を2等分する
とくにベクトルに関係する事項は(4)(5)になります。
(4)をベクトルで表すと、
\(\overrightarrow{AB}=\overrightarrow{DC}\) (\(\overrightarrow{AD}=\overrightarrow{BC}\)でもよい)
となります。向きと大きさが同じになるからです。
なお以下のことに注意してください。
平行四辺形\(ABCD\)と表記されていたら頂点\(A→B→C→D\)の順に線で結んでできる平行四辺形になり、1通りに決まります(他の平面図形も同様)。これに対して4点\(A,B,C,D\)を結ぶ平行四辺形という表記の場合は、結び方が複数パターン考えられるので、平行四辺形も複数パターン(全部で3つ)あります。詳しくは演習で扱います。
(例題1)
3点 \(A(0,2)\), \(B(-1,-1)\), \(C(3,0)\) がある。
(1)四角形\(ABCD\)が平行四辺形であるとき、点\(D\)の座標を求めよ。
(2)3点\(A,B,C\)と、もう1つの点\(D\)を結んで平行四辺形を作る。第4の頂点\(D\)の座標を求めよ。
(解答)
(1)
よって、\(\overrightarrow{AB}=\overrightarrow{DC}\) (\(\overrightarrow{AD}=\overrightarrow{BC}\)でもよい) です。
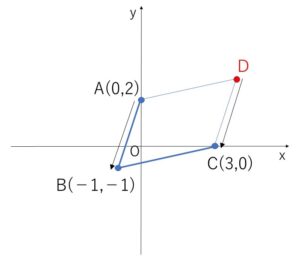
\(\overrightarrow{AB}=\overrightarrow{DC}\) より、\(D(x,y)\)として
\((-1-0,-1-2)=(3-x,-y)\)
\((-1,-3)=(3-x,-y)\)
\(-1=3-x\), \(-3=-y\) より
\(x=4\), \(y=3\)
よって \(D(4,3)\)
(2)
まず3点\(A,B,C\)から選んで2つの線分を作ると、
(i)\(AB,BC\) (ii)\(BC,CA\) (iii)\(CA,AB\) の3パターンの結び方があり、それぞれについて\(D\)が1つ決定するので、平行四辺形は全部で3つできます。なお(i)のパターンは(1)と同じになります。
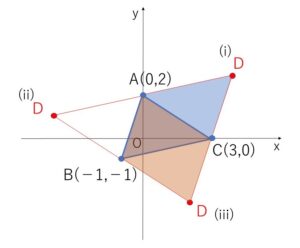
\(D(x,y)\) とおく
(i)平行四辺形\(ABCD\)の場合
(1)と同様なので \(D(4,3)\)
(ii)平行四辺形\(BCAD\)の場合
\(\overrightarrow{CA}=\overrightarrow{BD}\)
\((-3,2)=(x+1,y+1)\)
\(x+1=-3\), \(y+1=2\) より
\(x=-4\), \(y=1\)
よって \(D(-4,1)\)
(iii)平行四辺形\(CABD\)の場合
\(\overrightarrow{CA}=\overrightarrow{DB}\)
\((-3,2)=(-1-x,-1-y)\)
\(-1-x=-3\), \(-1-y=2\) より
\(x=2\), \(y=-3\)
よって \(D(2,-3)\)
(例題2)
四角形\(ABCD\)について、次のことを証明せよ。
四角形\(ABCD\)が平行四辺形 \(⇔\) \(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{AD}\)
(解答)
(ア)四角形\(ABCD\)が平行四辺形 \(→\) \(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{AD}\)・・・(※) について
(平行四辺形であることは決まっているので、それを利用して(※)を導きます)
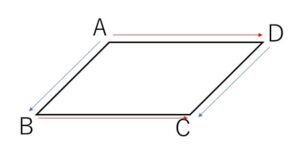
四角形\(ABCD\)が平行四辺形なので
\(\overrightarrow{BC}=\overrightarrow{AD}\)
((※)の左辺)\(=\overrightarrow{AC}+\overrightarrow{BD}\)
\(=\overrightarrow{AB}+\overrightarrow{BC}+(\overrightarrow{AD}-\overrightarrow{AB})\)
\(=\overrightarrow{BC}+\overrightarrow{AD}\)
\(=2\overrightarrow{AD}\)
\(=((※)の右辺)\)
\(=\overrightarrow{AC}+\overrightarrow{BD}\)
\(=\overrightarrow{AB}+\overrightarrow{BC}+(\overrightarrow{BC}+\overrightarrow{CD})\)
(\(\overrightarrow{AB}=-\overrightarrow{CD}\)より)
\(=2\overrightarrow{BC}\)
\(=2\overrightarrow{AD}\)
などと変形してもよいです。
(イ)\(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{AD}\)・・・(※) \(→\) 四角形\(ABCD\)が平行四辺形 について
(今度は等式(※)から平行四辺形であることを導きます)
(※)より
\((\overrightarrow{AB}+\overrightarrow{BC})+(\overrightarrow{AD}-\overrightarrow{AB})=2\overrightarrow{AD}\)
整理すると
\(\overrightarrow{BC}=\overrightarrow{AD}\)
したがって1組の対辺が平行で長さが等しいので、平行四辺形となる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ベクトルの1次独立と分解 back→ベクトルの平行②