\(\require{cancel}\)
ベクトルの1次独立について学んでいきます。
参考書の1次独立の定義に関する事項は書籍によって違う場合がありますが、自分なりに納得できるもので定着させてください。
・ベクトルの1次独立
ベクトル \(\vec{v_1},\vec{v_2},\cdots,\vec{v_r}\) のうち1つのベクトルが残りのベクトルの実数倍の和(1次結合という)で表されるとき、これらのベクトルの組は1次従属であるといい、
\(\vec{v_1},\vec{v_2},\cdots,\vec{v_r}\) のどのベクトルも残りのベクトルの実数倍の和で表すことができない場合、これらのベクトルの組は1次独立であるといいます。
以下平面におけるベクトルについて考えていきます。
\(r=2\) として2つのベクトル \(\vec{a},\vec{b}\) について、\(\vec{a},\vec{b}\) が1次独立であるとします。
\(\vec{a}=0\) とすると、\(\vec{a}=0\cdot\vec{b}\) と表されるので矛盾。よって\(\vec{a}≠0\)。
同様に\(\vec{b}≠0\)
また、\(\vec{a},\vec{b}\) が平行であるとすると \(\vec{a}=k\vec{b}\) と表されるので矛盾。
よって
\(\vec{a},\vec{b}\) が1次独立 \(→\) \(\vec{a}≠0\), \(\vec{b}≠0\), \(\vec{a}\bcancel{/\!/}\vec{b}\)
逆に \(\vec{a}≠0\), \(\vec{b}≠0\), \(\vec{a}\bcancel{/\!/}\vec{b}\) のとき
\(\vec{a}=k\vec{b}\) または \(\vec{b}=k\vec{a}\) と表されることはないので
\(\vec{a}≠0\), \(\vec{b}≠0\), \(\vec{a}\bcancel{/\!/}\vec{b}\) \(→\) \(\vec{a},\vec{b}\) が1次独立
したがって次の重要なことが成り立ちます。
\(\vec{a},\vec{b}\) が1次独立 \(⇔\) \(\vec{a}≠0\), \(\vec{b}≠0\), \(\vec{a}\bcancel{/\!/}\vec{b}\)
そして\(\vec{a},\vec{b}\)が1次独立のときには、
(1)任意の平面ベクトル\(\vec{p}\)を\(\vec{a},\vec{b}\)で表せる。
(2)その表し方は1通りしかない
ということが成り立ちます。平行でない2つのベクトル(\(\vec{0}\)でない)を用いれば、図を考えると感覚的には(1)(2)が成り立つよう気がすると思いますが少し丁寧に考えると次の通りです。
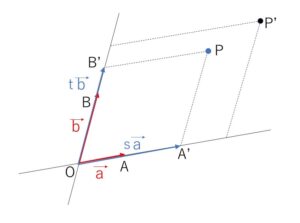
\(\vec{a}=\overrightarrow{OA}\), \(\vec{b}=\overrightarrow{OB}\) とする。
任意の点\(P\)において、\(P\)を通り\(OA\)に平行な直線と直線\(OB\)との交点を\(B’\)、\(P\)を通り\(OB\)に平行な直線と直線\(OA\)との交点を\(A’\)とする。
\(s,t\)を実数として、\(\overrightarrow{OA’}=s\vec{a}\), \(\overrightarrow{OB’}=t\vec{b}\) と表されるので、\(\overrightarrow{OP}=\vec{p}\) とすると
\(\vec{p}=\overrightarrow{OA’}+\overrightarrow{OB’}\)\(=s\vec{a}+t\vec{b}\)
と任意の\(\vec{p}\)を\(\vec{a},\vec{b}\)の実数倍の和で表すことができる。
また、\(\overrightarrow{OP’}=s’\vec{a}+t’\vec{b}\) として同様に\(P’\)を通る\(OA,OB\)に平行な直線を考えると、\(s’≠s\) もしくは \(t’≠t\) のとき図より\(P’\)と\(P\)は異なる点になる。したがって、\(\vec{p}\)の表し方は1通りになる。
(成分表示だと)
\(\vec{a}=(a_1,a_2)\), \(\vec{b}=(b_1,b_2)\), (\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\)) \(\vec{p}=(p_1,p_2)\) とすると
\(\vec{a}/\!/\vec{b}\) \(⇔\) \(a_1b_2-a_2b_1=0\) より
\(\vec{a}\bcancel{/\!/}\vec{b}\) \(⇔\) \(a_1b_2-a_2b_1≠0\) だから
\(\vec{p}=s\vec{a}+t\vec{b}\) を満たす実数\(s,t\)を求めると
\((p_1,p_2)=(sa_1+tb_1,sa_2+tb_2)\) より
\(sa_1+tb_1=p_1\)・・・①
\(sa_2+tb_2=p_2\)・・・②
①×\(b_2\)-②×\(b_1\) より
\(s(a_1b_2-a_2b_1)=p_1b_2-p_2b_1\)
\(a_1b_2-a_2b_1≠0\) より
\(s=\displaystyle\frac{p_1b_2-p_2b_1}{a_1b_2-a_2b_1}\)
①×\(a_2\)-②×\(a_1\) より
\(t(a_2b_1-a_1b_2)=p_1a_2-p_2a_1\)
\(a_1b_2-a_2b_1≠0\) より
\(t=\displaystyle\frac{p_1a_2-p_2a_1}{a_2b_1-a_1b_2}\)
したがって、任意の\(\vec{p}=(p_1,p_2)\) において上記のように\(s,t\)を設定すれば
\(\vec{p}=s\vec{a}+t\vec{b}\) の形で表せる。
また、\(s,t\)は \(\vec{p}=(p_1,p_2)\) を1つ決めればただ1通りに決まる。
また、\(\vec{p}=s\vec{a}+t\vec{b}\) の表し方は、\(\vec{p}\)を \(\vec{a},\vec{b}\) 方向に分けて表しているとみることができ、これを\(\vec{p}\)の\(\vec{a},\vec{b}\)方向への分解といいます。
ここで、\(\vec{a},\vec{b}\) が1次独立でない、例えば平行であるときは
\(s\vec{a}+t\vec{b}\) で表されるベクトルは、\(\vec{a}\)に平行(\(\vec{b}\)にも平行)なベクトルか\(\vec{0}\) だけとなる。
また、その表し方は無数にある。
\(\vec{a}=(1,2)\), \(\vec{b}=(2,4)\), \(\vec{p}=(3,6)\) とすると
\(\vec{p}=s\vec{a}+t\vec{b}=(s+2t)(1,2)\) より
\(s+2t=3\) を満たしていればよいので
\(\vec{p}=\vec{a}+\vec{b}\)
\(\vec{p}=5\vec{a}-\vec{b}\)
\(\vec{p}=2\vec{a}+\displaystyle\frac{1}{2}\vec{b}\)
など無数に存在する。
・1次独立なベクトルと係数
2つの1次独立なベクトル \(\vec{a},\vec{b}\) について次のことが成り立ちます。
\(\vec{a},\vec{b}\)が1次独立 \(⇔\) (I)を満たすのは \(s=t=0\) に限る
(証明)
(\(→\) について)
\(s≠0\) とすると、(I)より
\(\vec{a}=-\displaystyle\frac{t}{s}\vec{b}\) となり、1次独立であることに矛盾。
よって \(s=0\)
(I)より \(t\vec{b}=\vec{0}\)
\(\vec{b}≠\vec{0}\) だから
\(t=0\)
(\(←\) について)
\(\vec{a}=\vec{0}\) とすると、\(t=0\) のとき 任意の実数\(s\)で(I)が成り立つので矛盾。
よって \(\vec{a}≠0\)
同様に \(\vec{b}≠0\)
また、\(\vec{a}/\!/\vec{b}\) とすると、\(\vec{a}=k\vec{b}\) と表せるから (I)より
\(sk\vec{b}+t\vec{b}=\vec{0}\)
\((sk+t)\vec{b}=\vec{0}\)・・・③
例えば\(s=1\), \(t=-k\) で③は成り立つので、\(s=t=0\) に限ることに矛盾。
したがって、\(\vec{a}\bcancel{/\!/}\vec{b}\)
ゆえに \(\vec{a},\vec{b}\) は1次独立。
そしてこの定理より次のことが成り立ちます。
\(s\vec{a}+t\vec{b}=s’\vec{a}+t’\vec{b}\) ならば \(s=s’\) かつ \(t=t’\)
(ベクトルの表し方の一意性からも成り立つことが分かります)
(証明)
\(s\vec{a}+t\vec{b}=s’\vec{a}+t’\vec{b}\) より
\((s-s’)\vec{a}+(t-t’)\vec{b}=\vec{0}\)
よって \(s-s’=0\) かつ \(t-t’=0\) だから
\(s=s’\) かつ \(t=t’\)
(注)
\(s\vec{a}+t\vec{b}=\vec{0}\)・・・(I) を満たす\(s,t\)は
\(\vec{a},\vec{b}\)が1次独立でない場合は、無数に存在する。
例えば\(\vec{a}=2\vec{b}\) のとき
\((2s+t)\vec{b}=\vec{0}\) より
\(s=1,t=-2\), \(s=-2,t=4\) など
また、係数比較もできない。
・1次独立を考える理由
ここまで1次独立に関する説明をしてきましたが、何故こんなことを考える必要があるかというと以下のようなことが重要だからです。
(1)ベクトルの等式で係数比較していいかどうか
(2)斜交座標
(3)複数のベクトルが登場するときの処理方法
まず(1)についてですが、これは今まで解説した通りです。
\(2\vec{a}+5\vec{b}=s\vec{a}+t\vec{b}\)
という等式があったとき、\(s=2\), \(t=5\) としていいのは\(\vec{a},\vec{b}\)が1次独立のときだでけです。
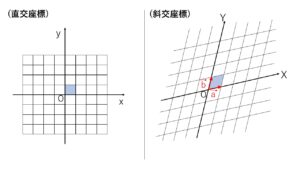
(2)については、馴染みがある\(xy\)平面(直交座標という)で考えるよりも、2つのベクトル\(\vec{a},\vec{b}\) 方向を軸とした座標(斜交座標) で考えた方が分かりやすいことがあります。
例えば軌跡・領域の問題などです。
(3)については、平面に関するベクトルなのに3つ以上のベクトルが問題に登場している場合は、そのうち2つのベクトルが1次独立だと、他のベクトルはすべてこの2つのベクトルで表すことができます。よって実質的には2つのベクトルのみで扱うことができるということになりますが、敢えて複数のベクトルのまま処理することもあります。
今回は例題はありません。
以上になります。お疲れさまでした。
此処まで見て頂きありがとうございました。
next→内積の定義 back→平行四辺形とベクトル