なす角

2つのベクトルのなす角に関する問題について見ていきます。

(例題1)
(1)\(\vec{a}=(1,5)\), \(\vec{b}=(3,2)\) のなす角\(θ\)を求めよ。
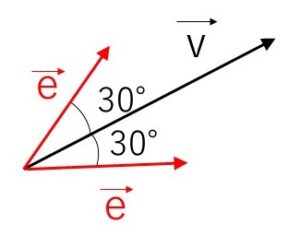
(2)ベクトル \(\vec{v}=(\sqrt{3},1)\) と \(30°\) の角をなす単位ベクトル \(\vec{e}\) を求めよ。

(解答)
(1)
\(\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cosθ\) より
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\)

\(\cosθ=\displaystyle\frac{1\cdot3+5\cdot2}{\sqrt{1^2+5^2}\sqrt{3^2+2^2}}\)
\(=\displaystyle\frac{13}{\sqrt{26}\sqrt{13}}\)
\(=\displaystyle\frac{1}{\sqrt{2}}\)

\(0°≦θ≦180°\) だから
\(θ=45°\)

(2)

\(\vec{e}=(x,y)\) とおくと大きさが\(1\)だから

\(\sqrt{x^2+y^2}=1\)・・・①

また、\(\vec{v}=(\sqrt{3},1)\) とのなす角が \(30°\) だから

\(\vec{v}\cdot\vec{e}=|\vec{v}||\vec{e}|\cos30°\)
\(\sqrt{3}x+1\cdot y=\sqrt{3+1}\cdot1\cdot\displaystyle\frac{\sqrt{3}}{2}\)・・・②

①より
\(x^2+y^2=1\)・・・③
②より
\(\sqrt{3}x+y=\sqrt{3}\)・・・④

④より \(y=\sqrt{3}(-x+1)\)・・・⑤
③に代入して
\(x^2+3(-x+1)^2=1\)
\(2x^2-3x+1=0\)
\((2x-1)(x-1)=0\)
\(x=\displaystyle\frac{1}{2},1\)

⑤より
\(x=\displaystyle\frac{1}{2}\) のとき \(y=\displaystyle\frac{\sqrt{3}}{2}\)
\(x=1\) のとき \(y=0\)

よって
\(\vec{e}=(\displaystyle\frac{1}{2},\displaystyle\frac{\sqrt{3}}{2}),(1,0)\)

図からも条件を満たす単位ベクトルが2つあることが分かります。

(例題2)
\(|\vec{a}|=1\), \(|\vec{b}|=2\), \(|2\vec{a}-\vec{b}|=\sqrt{6}-\sqrt{2}\) のとき、2つのベクトル \(\vec{a},\vec{b}\) のなす角\(θ\)を求めよ。

(解答)
\(|2\vec{a}-\vec{b}|^2=(\sqrt{6}-\sqrt{2})^2\) より
\((2\vec{a}-\vec{b})\cdot(2\vec{a}-\vec{b})=(\sqrt{6}-\sqrt{2})^2\)

(最初なので丁寧に展開してみます)

\(4\vec{a}\cdot\vec{a}-2\vec{a}\cdot\vec{b}-2\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{b}=6-2\sqrt{12}+2\)
\(4|\vec{a}|^2-4\vec{a}\cdot\vec{b}+|\vec{b}|^2=8-4\sqrt{3}\)

\(|\vec{a}|=1\), \(|\vec{b}|=2\) より
\(4-4\vec{a}\cdot\vec{b}+4=8-4\sqrt{3}\)
よって
\(\vec{a}\cdot\vec{b}=\sqrt{3}\)

したがって
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\displaystyle\frac{\sqrt{3}}{1\cdot2}=\displaystyle\frac{\sqrt{3}}{2}\)

ゆえに \(θ=30°\)

(例題3)
3つのベクトル、\(\vec{a},\vec{b},\vec{c}\) が次の条件を満たすとき、\(\vec{a},\vec{b}\)のなす角\(θ_1,θ_2\)をそれぞれ求めよ。

(1)\(\vec{a}+\vec{b}+\vec{c}=\vec{0}\) かつ \(|\vec{a}|=|\vec{b}|=|\vec{c}|=1\) 　 のとき \(θ_1\)

(2)\(\vec{a}+\vec{b}+\vec{c}=\vec{0}\) かつ \(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=-1\)　のとき \(θ_2\)

(1)

(解法1) (移項して2乗する方法)

\(\vec{a}+\vec{b}=-\vec{c}\) より、両辺大きさの2乗をとると
\(|\vec{a}+\vec{b}|^2=|-\vec{c}|^2\)

\(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2=|\vec{c}|^2\)　(\(-\vec{c}\) と \(\vec{c}\) の大きさは同じ)

\(|\vec{a}|=|\vec{b}|=|\vec{c}|=1\) より
\(1+2\vec{a}\cdot\vec{b}+1=1\)
\(\vec{a}\cdot\vec{b}=-\displaystyle\frac{1}{2}\)

したがって
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=-\displaystyle\frac{1}{2}\)

ゆえに \(θ=120°\)

(解法2) (両辺にベクトルを掛ける方法)

\(\vec{a}+\vec{b}+\vec{c}=\vec{0}\) の両辺について、\(\vec{a}\)との内積をとると

\(|\vec{a}|^2+\vec{a}\cdot\vec{b}+\vec{c}\cdot\vec{a}=0\)・・・①

同様に \(\vec{b},\vec{c}\) との内積をとると

\(\vec{a}\cdot\vec{b}+|\vec{b}|^2+\vec{b}\cdot\vec{c}=0\)・・・②
\(\vec{c}\cdot\vec{a}+\vec{b}\cdot\vec{c}+|\vec{c}|^2=0\)・・・③

\(|\vec{a}|=|\vec{b}|=|\vec{c}|=1\) より ①～③は

\(1+\vec{a}\cdot\vec{b}+\vec{c}\cdot\vec{a}=0\)・・・④
\(\vec{a}\cdot\vec{b}+1+\vec{b}\cdot\vec{c}=0\)・・・⑤
\(\vec{c}\cdot\vec{a}+\vec{b}\cdot\vec{c}+1=0\)・・・⑥

④+⑤+⑥より
\(3+2(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a})=0\)
\(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a}=-\displaystyle\frac{3}{2}\)・・・⑦

⑦－⑥ より
\(\vec{a}\cdot\vec{b}-1=-\displaystyle\frac{3}{2}\)
\(\vec{a}\cdot\vec{b}=-\displaystyle\frac{1}{2}\)

(以下(解法1)と同様です)

(2)

(解法1) (両辺にベクトルを掛ける方法)

\(\vec{a}+\vec{b}+\vec{c}=\vec{0}\) の両辺と \(\vec{a}\) または \(\vec{b}\) の内積をとると
(\(\vec{c}\)との内積は今回必要ないです)

\(|\vec{a}|^2+\vec{a}\cdot\vec{b}+\vec{c}\cdot\vec{a}=0\)
\(\vec{a}\cdot\vec{b}+|\vec{b}|^2+\vec{b}\cdot\vec{c}=0\)

\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=-1\) より

\(|\vec{a}|^2-1-1=0\)
\(-1+|\vec{b}|^2-1=0\)

よって
\(|\vec{a}|=|\vec{b}|=\sqrt{2}\)

したがって
\(\cosθ=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}=\displaystyle\frac{-1}{\sqrt{2}\sqrt{2}}=-\displaystyle\frac{1}{2}\)

ゆえに \(θ=120°\)

(解法2) (移項して2乗する方法)

\(\vec{a}+\vec{b}+\vec{c}=\vec{0}\) より

\(\vec{a}+\vec{b}=-\vec{c}\)
\(\vec{b}+\vec{c}=-\vec{a}\)
\(\vec{c}+\vec{a}=-\vec{b}\)

大きさの2乗を考えて

\(|\vec{a}+\vec{b}|^2=|-\vec{c}|^2\)
\(|\vec{b}+\vec{c}|^2=|-\vec{a}|^2\)
\(|\vec{c}+\vec{a}|^2=|-\vec{b}|^2\)

\(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2=|\vec{c}|^2\)
\(|\vec{b}|^2+2\vec{b}\cdot\vec{c}+|\vec{c}|^2=|\vec{a}|^2\)
\(|\vec{c}|^2+2\vec{c}\cdot\vec{a}+|\vec{a}|^2=|\vec{b}|^2\)

\(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}=-1\) を代入して整理すると

\(|\vec{a}|^2+|\vec{b}|^2-|\vec{c}|^2=2\)・・・(i)
\(-|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2=2\)・・・(ii)
\(|\vec{a}|^2-|\vec{b}|^2+|\vec{c}|^2=2\)・・・(iii)

(i)+(ii) より
\(2|\vec{b}|^2=4\)　\(|\vec{b}|=\sqrt{2}\)

(i)+(iii) より
\(2|\vec{a}|^2=4\)　\(|\vec{a}|=\sqrt{2}\)

(以下(解法1)と同様)

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→平行・垂直条件　back→内積の計算