\(\require{cancel}\)
交点の位置ベクトルに関する問題について見ていきます。
①2通りに表して係数比較(ただし1次独立であることは確認する)
②交点は2直線どちらの上にもある(係数の和が1を使う)
のいずれかを利用することになります。②で必要な知識があるので例題に入る前に整理しておきます。
・点\(P\)が直線\(AB\)上にある条件
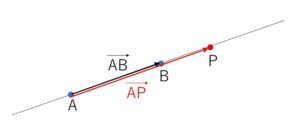
以前にも触れましたが、異なる2点\(A,B\)に対して点\(P\)が直線\(AB\)上にある条件は、\(\overrightarrow{AP}/\!/\overrightarrow{AB}\) または \(\overrightarrow{AP}=\vec{0}\) より
点\(P\)が直線\(AB\)上にある \(⇔\) \(\overrightarrow{AP}=k\overrightarrow{AB}\)・・・① (\(k\)は実数)
となります。ここで、\(P(\vec{p})\), \(A(\vec{a})\), \(B(\vec{b})\) とおくと①は
\(\vec{p}-\vec{a}=k(\vec{b}-\vec{a})\)
整理すると
\(\vec{p}=(1-k)\vec{a}+k\vec{b}\)
となるので
点\(P\)が直線\(AB\)上にある \(⇔\) \(\vec{p}=(1-k)\vec{a}+k\vec{b}\)・・・② (\(k\)は実数)
さらに②の右辺の係数の和が \((1-k)+k=1\) となることに着目して
\(1-k=s\), \(k=t\) とおくと
点\(P\)が直線\(AB\)上にある \(⇔\) \(\vec{p}=s\vec{a}+t\vec{b}\)・・・③ かつ \(s+t=1\) (\(s,t\)は実数)
となります。
\(P\)が\(AB\)上にあって、\(\vec{p}=s\vec{a}+t\vec{b}\) という形になっていれば、係数の和が \(s+t=1\) になります(2直線どちらの上にもある解法で使う)。
なお\(P\)が直線\(AB\)上にあるので、内分点,外分点どちらも②③の形で表せます。
(例題)
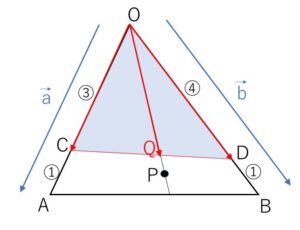
三角形\(OAB\)の2辺 \(OA,OB\) をそれぞれ \(3:1\), \(4:1\) に内分する点を\(C,D\)とし、\(BC\)と\(AD\)の交点を\(P\), \(CD\)と\(OP\)の交点を\(Q\)とする。ベクトル \(\overrightarrow{OA},\overrightarrow{OB}\) をそれぞれ \(\vec{a},\vec{b}\) とおくとき、次の問いに答えよ。
(1)\(\overrightarrow{OP}\)を\(\vec{a},\vec{b}\) を使って表せ。
(2)\(\overrightarrow{OQ}\)を\(\vec{a},\vec{b}\) を使って表せ。
(解答)
(1-1)係数比較の方法
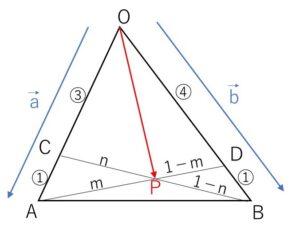
\(AP:PD=m:1-m\), \(CP:PB=n:1-n\) とおくと、
\(\overrightarrow{OP}=(1-m)\overrightarrow{OA}+m\overrightarrow{OD}\)
\(\overrightarrow{OP}=(1-n)\overrightarrow{OC}+n\overrightarrow{OB}\)
\(\overrightarrow{OD}=\displaystyle\frac{4}{5}\vec{b}\), \(\overrightarrow{OC}=\displaystyle\frac{3}{4}\vec{a}\) より
\(\overrightarrow{OP}=(1-m)\vec{a}+\displaystyle\frac{4}{5}m\vec{b}\)・・・①
\(\overrightarrow{OP}=\displaystyle\frac{3}{4}(1-n)\vec{a}+n\vec{b}\)・・・②
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\), \(\vec{a}\bcancel{/\!/}\vec{b}\) (1次独立) より①②の係数を比較して
\(1-m=\displaystyle\frac{3}{4}(1-n)\)
\(\displaystyle\frac{4}{5}m=n\)
よって
\(m=\displaystyle\frac{5}{8}\), \(n=\displaystyle\frac{1}{2}\)
①から
\(\overrightarrow{OP}=\displaystyle\frac{3}{8}\vec{a}+\displaystyle\frac{1}{2}\vec{b}\)
(1-2)係数の和が1を利用する方法
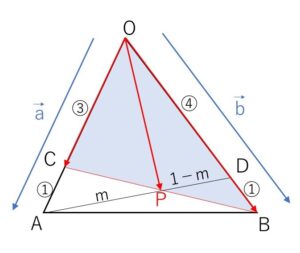
点\(P\)は\(AD\)上にあるので、\(AP:PD=m:1-m\) とおくと、
\(\overrightarrow{OP}=(1-m)\overrightarrow{OA}+m\overrightarrow{OD}\)・・・③
係数の和が1であることを利用するために、③の\(\overrightarrow{OA},\overrightarrow{OD}\) を、\(\overrightarrow{OC},\overrightarrow{OB}\) に変えます。
ここで
\(\overrightarrow{OC}=\displaystyle\frac{3}{4}\overrightarrow{OA}\) (\(\overrightarrow{OA}=\displaystyle\frac{4}{3}\overrightarrow{OC}\)), \(\overrightarrow{OD}=\displaystyle\frac{4}{5}\overrightarrow{OB}\) を③に代入して
\(\overrightarrow{OP}=\displaystyle\frac{4}{3}(1-m)\overrightarrow{OC}+\displaystyle\frac{4}{5}m\overrightarrow{OB}\)・・・④
点\(P\)は\(BC\)上の点でもあるから④より
\(\displaystyle\frac{4}{3}(1-m)+\displaystyle\frac{4}{5}m=1\)
これを解くと
\(m=\displaystyle\frac{5}{8}\)
③から
\(\overrightarrow{OP}=\displaystyle\frac{3}{8}\overrightarrow{OA}+\displaystyle\frac{5}{8}\overrightarrow{OD}\)
\(=\displaystyle\frac{3}{8}\overrightarrow{OA}+\displaystyle\frac{5}{8}\cdot\displaystyle\frac{4}{5}\overrightarrow{OB}\)
\(=\displaystyle\frac{3}{8}\vec{a}+\displaystyle\frac{1}{2}\vec{b}\)
(2-1)係数比較の方法
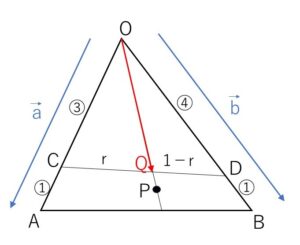
点\(Q\)は\(CD\)上にあるので、\(CQ:QD=r:1-r\) とおくと
\(\overrightarrow{OQ}=(1-r)\overrightarrow{OC}+r\overrightarrow{OD}\)
\(=\displaystyle\frac{3}{4}(1-r)\vec{a}+\displaystyle\frac{4}{5}r\vec{b}\)・・・(i)
また、点\(Q\)は\(OP\)上にあるので(1)より
\(\overrightarrow{OQ}=k\overrightarrow{OP}\)\(=\displaystyle\frac{3}{8}k\vec{a}+\displaystyle\frac{1}{2}k\vec{b}\)・・・(ii)
\(\vec{a}≠\vec{0}\), \(\vec{b}≠\vec{0}\), \(\vec{a}\bcancel{/\!/}\vec{b}\) (1次独立) より(i)(ii)の係数を比較して
\(\displaystyle\frac{3}{4}(1-r)=\displaystyle\frac{3}{8}k\)
\(\displaystyle\frac{4}{5}r=\displaystyle\frac{1}{2}k\)
\(r=\displaystyle\frac{5}{9}\), \(k=\displaystyle\frac{8}{9}\)
(ii)より
\(\overrightarrow{OQ}=\displaystyle\frac{1}{3}\vec{a}+\displaystyle\frac{4}{9}\vec{b}\)
(2-2)係数の和が1を利用する方法
点\(Q\)は\(OP\)上にあるので
\(\overrightarrow{OQ}=k\overrightarrow{OP}=\displaystyle\frac{3}{8}k\vec{a}+\displaystyle\frac{1}{2}k\vec{b}\)・・・(iii)
\(\overrightarrow{OC}=\displaystyle\frac{3}{4}\vec{a}\), \(\overrightarrow{OD}=\displaystyle\frac{4}{5}\vec{b}\)
つまり
\(\vec{a}=\displaystyle\frac{4}{3}\overrightarrow{OC}\), \(\vec{b}=\displaystyle\frac{5}{4}\overrightarrow{OD}\) より
\(\overrightarrow{OQ}=\displaystyle\frac{3}{8}k\cdot\displaystyle\frac{4}{3}\overrightarrow{OC}+\displaystyle\frac{1}{2}k\cdot\displaystyle\frac{5}{4}\overrightarrow{OD}\)
\(=\displaystyle\frac{1}{2}k\overrightarrow{OC}+\displaystyle\frac{5}{8}k\overrightarrow{OD}\)
点\(Q\)は\(CD\)上にもあるから
\(\displaystyle\frac{1}{2}k+\displaystyle\frac{5}{8}k=1\)
これを解くと
\(k=\displaystyle\frac{8}{9}\)
(iii)より
\(\overrightarrow{OQ}=\displaystyle\frac{3}{8}k\vec{a}+\displaystyle\frac{1}{2}k\vec{b}\)
\(=\displaystyle\frac{1}{3}\vec{a}+\displaystyle\frac{4}{9}\vec{b}\)
一方係数比較の場合は計算が面倒になることが多いですが使える範囲は広いです。ただし1次独立の確認は必要です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→角の2等分線とベクトル back→点Pの位置ベクトル