三角形の内接円とベクトル

内接円(内心)とベクトルに関する例題について見ていきます。

(例題1)
\(△ABC\)において、頂点\(A,B,C\)の位置ベクトルを\(\vec{a},\vec{b},\vec{c}\)とし、辺の長さを \(BC=a\), \(CA=b\), \(AB=c\) とする。\(△ABC\)の内接円の中心\(P\)の位置ベクトルは
\(\vec{p}=\displaystyle\frac{a\vec{a}+b\vec{b}+c\vec{c}}{a+b+c}\)　で与えられることを示せ。

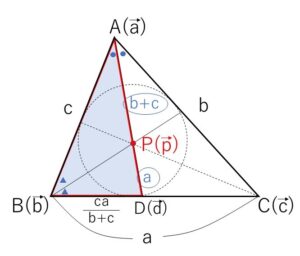
内接円の中心は、内角の2等分線の交点である。
角\(A\)の2等分線と\(BC\)の交点を\(D(\vec{d})\)とすると

\(BD=\displaystyle\frac{c}{c+b}×a=\displaystyle\frac{ca}{b+c}\)

また
\(AP:PD\)
\(=BA:BD\)
\(=c:\displaystyle\frac{ca}{b+c}\)
\(=(b+c):a\)

ここで \(\vec{d}=\displaystyle\frac{b\vec{b}+c\vec{c}}{c+b}\)　だから

\(\vec{p}=\displaystyle\frac{a\vec{a}+(b+c)\vec{d}}{(b+c)+a}\)

\(=\displaystyle\frac{a\vec{a}+(b+c)\cdot\displaystyle\frac{b\vec{b}+c\vec{c}}{c+b}}{(b+c)+a}\)

\(=\displaystyle\frac{a\vec{a}+b\vec{b}+c\vec{c}}{a+b+c}\)

(例題2)
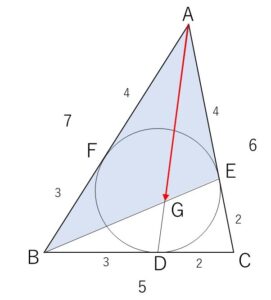
三角形\(ABC\)において、\(BC=5\), \(CA=6\), \(AB=7\) とする。この三角形の内接円と辺\(BC,CA,AB\)の接点をそれぞれ\(D,E,F\)とする。また線分\(BE\)と線分\(AD\)の交点を\(G\)とする。\(\overrightarrow{AB}=\vec{p}\),　\(\overrightarrow{AC}=\vec{q}\) として

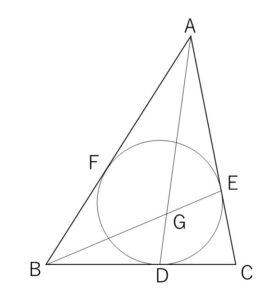
(1)\(\overrightarrow{AD}\)を\(\vec{p},\vec{q}\)を用いて表せ。
(2)\(\overrightarrow{AG}\)を\(\vec{p},\vec{q}\)を用いて表せ。
(3)3点 \(C,G,F\) は1直線上にあることを示せ。

(注)\(AD\) (\(BE\)) は角の2等分線ではありません。
内心を\(I\)とすると、\(AI\)が角の2等分線になりますが、\(AI\)と\(BC\)が垂直でないことと(2等辺三角形なら垂直になる)、\(ID \perp BC\) から \(A,I,D\) は1直線上にはないです。よって\(AI\)と\(AD\)は別の直線です。

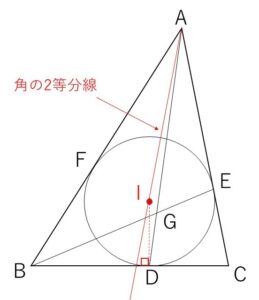
(解答)
(1)

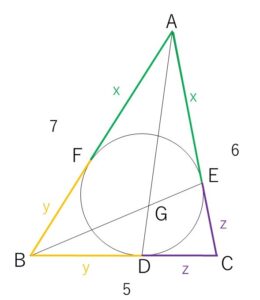
図より
\(x+y=7\),　\(y+z=5\),　\(z+x=6\)

これらの連立方程式を解いて
\(x=4\), \(y=3\), \(z=2\)

したがって
\(\overrightarrow{AD}=\displaystyle\frac{2\vec{p}+3\vec{q}}{3+2}\)
\(=\displaystyle\frac{2}{5}\vec{p}+\displaystyle\frac{3}{5}\vec{q}\)

(2)

\(\overrightarrow{AG}=k\overrightarrow{AD}\)
\(=\displaystyle\frac{2}{5}k\vec{p}+\displaystyle\frac{3}{5}k\vec{q}\)・・・①
\(=\displaystyle\frac{2}{5}k\vec{p}+\displaystyle\frac{3}{5}k(\displaystyle\frac{3}{2}\overrightarrow{AE})\)　(\(AC=\displaystyle\frac{3}{2}AE\) より)
\(=\displaystyle\frac{2}{5}k\overrightarrow{AB}+\displaystyle\frac{9}{10}k\overrightarrow{AE}\)

\(G\)は\(BE\)上にあるので
\(\displaystyle\frac{2}{5}k+\displaystyle\frac{9}{10}k=1\)
よって
\(k=\displaystyle\frac{10}{13}\)

①より
\(\overrightarrow{AG}=\displaystyle\frac{2}{5}k\vec{p}+\displaystyle\frac{3}{5}k\vec{q}\)

\(=\displaystyle\frac{4}{13}\vec{p}+\displaystyle\frac{6}{13}\vec{q}\)

(3)

\(\overrightarrow{CF}=\overrightarrow{AF}-\overrightarrow{AC}\)
\(=\displaystyle\frac{4}{7}\vec{p}-\vec{q}\)
\(=\displaystyle\frac{1}{7}(4\vec{p}-7\vec{q})\)

\(\overrightarrow{CG}=\overrightarrow{AG}-\overrightarrow{AC}\)
\(=(\displaystyle\frac{4}{13}\vec{p}+\displaystyle\frac{6}{13}\vec{q})-\vec{q}\)
\(=\displaystyle\frac{1}{13}(4\vec{p}-7\vec{q})\)

よって
\(\overrightarrow{CF}=\displaystyle\frac{13}{7}\overrightarrow{CG}\)

したがって \(C,G,F\) は一直線上にある。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の垂心とベクトル　back→角の2等分線とベクトル