三角形の垂心とベクトル | 教えて数学理科

三角形の垂心とベクトル、ベクトルの直交の問題について見ていきます。

(例題1)
三角形\(ABC\)において、\(|\overrightarrow{AB}|=4\), \(|\overrightarrow{AC}|=5\), \(|\overrightarrow{BC}|=6\) である。辺\(AC\)上の点\(D\)は \(BD \perp AC\) をみたし、辺\(AB\)上の点\(E\)は \(CE \perp AB\) をみたす。\(CE\)と\(BD\)の交点を\(H\)とする。

(1)\(\overrightarrow{AD}=r\overrightarrow{AC}\) となる実数\(r\)を求めよ。
(2)\(\overrightarrow{AH}=s\overrightarrow{AB}+t\overrightarrow{AC}\) となる実数\(s,t\)を求めよ。

垂直なので、「内積=0」を利用します。
内積の計算をするので、\(\overrightarrow{AB},\overrightarrow{AC}\)をそれぞれ\(\vec{b},\vec{c}\) とおくと、内積 \(\vec{b}\cdot\vec{c}\) が必要になっていきます。\(\vec{b}\cdot\vec{c}\) は \(|\overrightarrow{BC}|^2=36\) を変形するか、余弦定理から求めることができます。
なお\(H\)は三角形\(ABC\)の垂心です。

(解答)
(1)

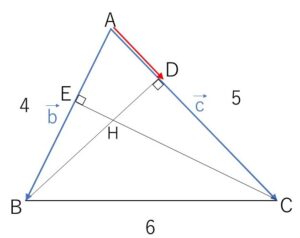
垂心　ベクトル例題1-1

\(\overrightarrow{AB}=\vec{b}\), \(\overrightarrow{AC}=\vec{c}\) とおく。

\(|\overrightarrow{BC}|^2=36\) より
\(|\vec{c}-\vec{b}|^2=36\)
\(|\vec{c}|^2-2\vec{b}\cdot\vec{c}+|\vec{b}|^2=36\)
\(25-2\vec{b}\cdot\vec{c}+16=36\)
よって
\(\vec{b}\cdot\vec{c}=\displaystyle\frac{5}{2}\)

\(\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}\)
\(=r\vec{c}-\vec{b}\)

\(\overrightarrow{BD} \perp \overrightarrow{AC}\) より　\(\overrightarrow{BD}\cdot\overrightarrow{AC}=0\)
\((r\vec{c}-\vec{b})\cdot\vec{c}=0\)
\(r|\vec{c}|^2-\vec{b}\cdot\vec{c}=0\)
\(25r-\displaystyle\frac{5}{2}=0\)

したがって
\(r=\displaystyle\frac{1}{10}\)

(2)

同様に\(\overrightarrow{AE}\) も求めれば、あとはただの交点\(H\)に関するベクトルの問題です。「係数の和=1 か 2通りに表して係数比較」で解けます。

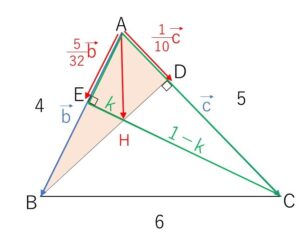
垂心ベクトル例題1-2

\(\overrightarrow{AE}=s\vec{b}\) とおくと
\(\overrightarrow{CE}=s\vec{b}-\vec{c}\) だから、(1)と同様に

\((s\vec{b}-\vec{c})\cdot\vec{b}=0\)
\(16s-\displaystyle\frac{5}{2}=0\)
\(s=\displaystyle\frac{5}{32}\)

\(H\)は\(EC\)上にあるので、\(EH:HC=k:(1-k)\) とおくと

\(\overrightarrow{AH}=(1-k)\cdot\displaystyle\frac{5}{32}\vec{b}+k\vec{c}\)・・・①

\(=\displaystyle\frac{5}{32}(1-k)\vec{b}+10k\cdot\displaystyle\frac{1}{10}\vec{c}\)

\(=\displaystyle\frac{5}{32}(1-k)\overrightarrow{AB}+10k\overrightarrow{AD}\)

\(H\)は\(BD\)上にもあるので
\(\displaystyle\frac{5}{32}(1-k)+10k=1\)
\(k=\displaystyle\frac{3}{35}\)

①より
\(\overrightarrow{AH}=(1-\displaystyle\frac{3}{35})\cdot\displaystyle\frac{5}{32}\vec{b}+\displaystyle\frac{3}{35}\vec{c}\)

\(=\displaystyle\frac{1}{7}\vec{b}+\displaystyle\frac{3}{35}\vec{c}\)

したがって
\(s=\displaystyle\frac{1}{7}\),　\(t=\displaystyle\frac{3}{35}\)

(例題2)
三角形\(ABC\)において、\(AB=3\), \(AC=2\) とする。辺\(BC\)を\(1:2\)の比に内分する点を\(D\)、辺\(CA\)を\(4:1\)の比に内分する点を\(E\)とし、直線\(AD\)と\(BE\)の交点を\(M\)とする。直線\(CM\)と辺\(AB\)の交点を\(F\)とする。また、直線\(CF\)が辺\(AB\)に直交するものとする。このとき

(1)\(\overrightarrow{CF}\)を\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)で表せ。
(2)\(△ABC\)の面積\(S\)を求めよ。
(3)\(A\)から辺\(BC\)に垂線を引き、それと直線\(CF\)との交点を\(G\)とするとき、線分\(AG\)の長さを求めよ。

(解答)
(1)

\(AD,BE\)の交点が\(M\)で、この交点\(M\)と\(C\)を結んだ直線と辺\(AB\)の交点が\(F\)です。よって、最後の直交条件の有無に関わらず、点\(F\)は決定します。
よって直交条件は使わずに、順序通りにまず\(\overrightarrow{AM}\)を求めて、\(\overrightarrow{CF}\)を求めていきます。

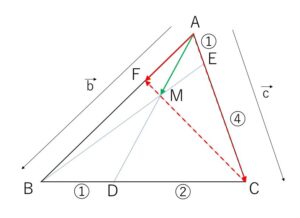
垂線ベクトル例題2-1

\(\overrightarrow{AB}=\vec{b}\),　\(\overrightarrow{AC}=\vec{c}\) とおく。

まず、\(\overrightarrow{AM}\)を求める。

\(M\)は\(AD\)上にあるので
\(\overrightarrow{AM}\)
\(=k\overrightarrow{AD}\)

\(=k\cdot\displaystyle\frac{2\vec{b}+\vec{c}}{1+2}\)

\(=\displaystyle\frac{2}{3}k\vec{b}+\displaystyle\frac{1}{3}k\vec{c}\)・・・①

\(=\displaystyle\frac{2}{3}k\vec{b}+\displaystyle\frac{5}{3}k\cdot\displaystyle\frac{1}{5}\vec{c}\)

\(=\displaystyle\frac{2}{3}k\overrightarrow{AB}+\displaystyle\frac{5}{3}k\overrightarrow{AE}\)

\(M\)は\(BE\)上にもあるので
\(\displaystyle\frac{2}{3}k+\displaystyle\frac{5}{3}k=1\)
\(k=\displaystyle\frac{3}{7}\)

よって①より
\(\overrightarrow{AM}=\displaystyle\frac{2}{7}\vec{b}+\displaystyle\frac{1}{7}\vec{c}\)

続いて\(\overrightarrow{CF}\)です。\(F\)は\(CM\)上にあるので
\(\overrightarrow{AF}=(1-m)\overrightarrow{AC}+m\overrightarrow{AM}\)・・・②
と表せることと、\(\overrightarrow{AF}\) は\(\vec{b}\)のみで表されることから\(m\)が決定できます。解答では\(C\)経由で\(\overrightarrow{AF}\)を求めますが、②と実質的に同じ式がでてきます。

ここで
\(\overrightarrow{AF}=\overrightarrow{AC}+m\overrightarrow{CM}\)

\(=\vec{c}+m\{(\displaystyle\frac{2}{7}\vec{b}+\displaystyle\frac{1}{7}\vec{c})-\vec{c}\}\)

\(=\displaystyle\frac{2}{7}m\vec{b}+(1-\displaystyle\frac{6}{7}m)\vec{c}\)・・・③

\(\overrightarrow{AF}=n\vec{b}\) と表されるから (\(\vec{b},\vec{c}\)は1次独立)
\(1-\displaystyle\frac{6}{7}m=0\)
\(m=\displaystyle\frac{7}{6}\)

よって③から
\(\overrightarrow{AF}=\displaystyle\frac{1}{3}\vec{b}\)

したがって
\(\overrightarrow{CF}=\overrightarrow{AF}-\overrightarrow{AC}\)
\(=\displaystyle\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AC}\)

(2)

面積\(S\)を求めるのに必要な情報は、2辺の長さは分かっているのであとは挟まれる角についてです(内積や三角比の値など)。内積 \(\vec{b}\cdot\vec{c}\) がまだ使っていない直交条件から求まります。

\(\overrightarrow{CF}\perp\overrightarrow{AB}\) より

\((\displaystyle\frac{1}{3}\vec{b}-\vec{c})\cdot\vec{b}=0\)
\(\displaystyle\frac{1}{3}|\vec{b}|^2-\vec{b}\cdot\vec{c}=0\)
\(\displaystyle\frac{1}{3}3^2-\vec{b}\cdot\vec{c}=0\)
よって
\(\vec{b}\cdot\vec{c}=3\)

したがって
\(S=\displaystyle\frac{1}{2}\sqrt{|\vec{b}|^2|\vec{c}|^2-(\vec{b}\cdot\vec{c})^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{3^2\cdot2^2-3^2}\)
\(=\displaystyle\frac{3\sqrt{3}}{2}\)

(3)

\(G\)が\(CF\)上にあることと、\(AG \perp BC\) から \(\overrightarrow{AG}\)が求まります。あとは \(|\overrightarrow{AG}|^2\) を計算するだけです。
なお\(G\)は三角形\(ABC\)の垂心です。

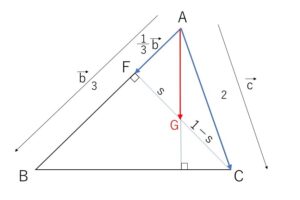
垂心ベクトル例題2-2

\(G\)は\(CF\)上にあるので
\(\overrightarrow{AG}=(1-s)\cdot\displaystyle\frac{1}{3}\vec{b}+s\vec{c}\)・・・④ とおける

\(\overrightarrow{AG}\perp\overrightarrow{BC}\) より
\(\{(1-s)\cdot\displaystyle\frac{1}{3}\vec{b}+s\vec{c}\}\cdot(\vec{c}-\vec{b})=0\)

(\(\vec{b}\cdot\vec{c}=3\),　\(|\vec{b}|^2=9\),　\(|\vec{c}|^2=4\) より)

\((1-s)-3(1-s)+4s-3s=0\)
よって
\(s=\displaystyle\frac{2}{3}\)

④より
\(\overrightarrow{AG}=\displaystyle\frac{1}{9}\vec{b}+\displaystyle\frac{2}{3}\vec{c}\)

\(|\overrightarrow{AG}|^2\)
\(=|\displaystyle\frac{1}{9}\vec{b}+\displaystyle\frac{2}{3}\vec{c}|^2\)

\(=\displaystyle\frac{1}{81}|\vec{b}|^2+\displaystyle\frac{4}{27}\vec{b}\cdot\vec{c}+\displaystyle\frac{4}{9}|\vec{c}|^2\)

\(=\displaystyle\frac{1}{9}+\displaystyle\frac{4}{9}+\displaystyle\frac{16}{9}\)

\(=\displaystyle\frac{21}{9}\)

したがって
\(AG=\displaystyle\frac{\sqrt{21}}{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→外接円・円周上の点とベクトル①　back→三角形の内接円とベクトル