外接円・円周上の点とベクトル①

外接円や円周上の点に関するベクトルの問題について見ていきます。

(例題1)
三角形\(ABC\)は、3辺の長さが
\(AB=1\), \(BC=\sqrt{6}\), \(CA=2\)
である。\(\overrightarrow{AB}=\vec{u}\), \(\overrightarrow{AC}=\vec{v}\) とすると

(1)内積 \(\vec{u}\cdot\vec{v}\) を求めよ。
(2)三角形\(ABC\)の外心(外接円の中心)を\(O\)とする。\(\overrightarrow{AO}=s\vec{u}+t\vec{v}\) となる実数\(s,t\)を求めよ。

(解答)
(1)

\(|\overrightarrow{BC}|^2=6\) より
\(|\vec{v}-\vec{u}|^2=6\)
\(|\vec{v}|^2-2\vec{v}\cdot\vec{u}+|\vec{u}|^2=6\)
\(4-2\vec{u}\cdot\vec{v}+1=6\)
よって
\(\vec{u}\cdot\vec{v}=-\displaystyle\frac{1}{2}\)

(2)

(解法i)

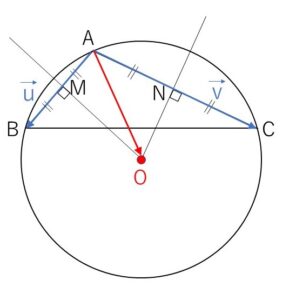
\(AB,AC\)の中点をそれぞれ\(M,N\)とする。

\(\overrightarrow{AM}=\displaystyle\frac{1}{2}\vec{u}\),　\(\overrightarrow{AC}=\displaystyle\frac{1}{2}\vec{v}\) より

\(\overrightarrow{MO}=s\vec{u}+t\vec{v}-\displaystyle\frac{1}{2}\vec{u}=(s-\displaystyle\frac{1}{2})\vec{u}+t\vec{v}\)
\(\overrightarrow{NO}=s\vec{u}+t\vec{v}-\displaystyle\frac{1}{2}\vec{v}=s\vec{u}+(t-\displaystyle\frac{1}{2})\vec{v}\)

\(\overrightarrow{AB}\perp\overrightarrow{MO}\),　\(\overrightarrow{AC}\perp\overrightarrow{NO}\) より

\(\vec{u}\cdot\{(s-\displaystyle\frac{1}{2})\vec{u}+t\vec{v}\}=0\)
\(\vec{v}\cdot\{s\vec{u}+(t-\displaystyle\frac{1}{2})\vec{v}\}=0\)

\((s-\displaystyle\frac{1}{2})\cdot1-\displaystyle\frac{1}{2}t=0\)
\(-\displaystyle\frac{1}{2}s+(t-\displaystyle\frac{1}{2})\cdot4=0\)

\(s-\displaystyle\frac{1}{2}t=\displaystyle\frac{1}{2}\)・・・①
\(-\displaystyle\frac{1}{2}s+4t=2\)・・・②

①②より
\(s=\displaystyle\frac{4}{5}\), \(t=\displaystyle\frac{3}{5}\)

(解法ii)
\(OA^2=OB^2=OC^2\) より

\(|-(s\vec{u}+t\vec{v})|^2=|\vec{u}-(s\vec{u}+t\vec{v})|^2=|\vec{v}-(s\vec{u}+t\vec{v})|^2\)

\(|s\vec{u}+t\vec{v}|^2=|(1-s)\vec{u}-t\vec{v}|^2=|-s\vec{u}+(1-t)\vec{v}|^2\)

左辺と中辺から
\(s^2|\vec{u}|^2+2st\vec{u}\cdot\vec{v}+t^2|\vec{v}|^2=(1-s)^2|\vec{u}|^2-2(1-s)t\vec{u}\cdot\vec{v}+t^2|\vec{v}|^2\)

(\(|\vec{u}|^2=1\),　\(|\vec{v}|^2=4\),　\(\vec{u}\cdot\vec{v}=-\displaystyle\frac{1}{2}\) より)

\(s^2-st+4t^2=(1-s)^2+(1-s)t+4t^2\)
整理して
\(0=1-2s+t\)・・・①’

左辺と右辺から
\(s^2|\vec{u}|^2+2st\vec{u}\cdot\vec{v}+t^2|\vec{v}|^2=s^2|\vec{u}|^2-2s(1-t)\vec{u}\cdot\vec{v}+(1-t)^2|\vec{v}|^2\)

\(s^2-st+4t^2=s^2+s(1-t)+4(1-t)^2\)
整理して
\(0=s+4-8t\)・・・②’

①’②’より
\(s=\displaystyle\frac{4}{5}\), \(t=\displaystyle\frac{3}{5}\)

(例題2)
平面上の点\(O\)を中心にもつ半径\(1\)の円周上に3点\(A,B,C\)がある。ベクトル間の関係式
\(3\overrightarrow{OA}+4\overrightarrow{OB}-5\overrightarrow{OC}=\vec{0}\)
が成り立つとき

(1)内積 \(\overrightarrow{OA}\cdot\overrightarrow{OB}\),　\(\overrightarrow{OB}\cdot\overrightarrow{OC}\),　\(\overrightarrow{OC}\cdot\overrightarrow{OA}\) の値を求めよ。
(2)三角形\(ABC\)の面積を求めよ。

(解答)
(1)

\(|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|=1\)

与式から
\(3\overrightarrow{OA}+4\overrightarrow{OB}=5\overrightarrow{OC}\) となるので
\(|3\overrightarrow{OA}+4\overrightarrow{OB}|^2=|5\overrightarrow{OC}|^2\)
\(9|\overrightarrow{OA}|+24\overrightarrow{OA}\cdot\overrightarrow{OB}+16|\overrightarrow{OB}|^2=25\)
\(9+24\overrightarrow{OA}\cdot\overrightarrow{OB}+16=25\)
よって
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=0\)

同様に与式から
\(4\overrightarrow{OB}-5\overrightarrow{OC}=-3\overrightarrow{OA}\) より
\(|4\overrightarrow{OB}-5\overrightarrow{OC}|^2=|-3\overrightarrow{OA}|^2\)
\(16-40\overrightarrow{OB}\cdot\overrightarrow{OC}+25=9\)
\(\overrightarrow{OB}\cdot\overrightarrow{OC}=\displaystyle\frac{4}{5}\)

\(3\overrightarrow{OA}-5\overrightarrow{OC}=-4\overrightarrow{OB}\)
\(|3\overrightarrow{OA}-5\overrightarrow{OC}|^2=|-4\overrightarrow{OB}|^2\)
\(9-30\overrightarrow{OA}\cdot\overrightarrow{OC}+25=16\)
\(\overrightarrow{OA}\cdot\overrightarrow{OC}=\displaystyle\frac{3}{5}\)

(2)

\(|\overrightarrow{AB}|^2=|\overrightarrow{OB}-\overrightarrow{OA}|^2\)
\(=|\overrightarrow{OB}|^2-2\overrightarrow{OB}\cdot\overrightarrow{OA}+|\overrightarrow{OA}|^2\)
\(=1+0+1\)
\(=2\)

\(|\overrightarrow{AC}|^2=|\overrightarrow{OC}-\overrightarrow{OA}|^2\)
\(=|\overrightarrow{OC}|^2-2\overrightarrow{OC}\cdot\overrightarrow{OA}+|\overrightarrow{OA}|^2\)
\(=1-2\cdot\displaystyle\frac{3}{5}+1\)
\(=\displaystyle\frac{4}{5}\)

\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
\(=(\overrightarrow{OB}-\overrightarrow{OA})\cdot(\overrightarrow{OC}-\overrightarrow{OA})\)
\(=\overrightarrow{OB}\cdot\overrightarrow{OC}-\overrightarrow{OB}\cdot\overrightarrow{OA}-\overrightarrow{OA}\cdot\overrightarrow{OC}+|\overrightarrow{OA}|^2\)
\(=\displaystyle\frac{4}{5}-0-\displaystyle\frac{3}{5}+1\)
\(=\displaystyle\frac{6}{5}\)

したがって
\(△ABC=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot\overrightarrow{AC})^2}\)

\(=\displaystyle\frac{1}{2}\sqrt{2\cdot\displaystyle\frac{4}{5}-(\displaystyle\frac{6}{5})^2}\)

\(=\displaystyle\frac{1}{5}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→外接円・円周上の点とベクトル②　back→三角形の垂心とベクトル