外接円・円周上の点とベクトル②

引き続き外接円(円周上の点)とベクトルの例題です。

(例題1)
三角形\(ABC\)の外心\(O\)から直線\(BC,CA,AB\)に下ろした垂線の足をそれぞれ\(P,Q,R\)とするとき、\(\overrightarrow{OP}+2\overrightarrow{OQ}+3\overrightarrow{OR}=\vec{0}\) が成立しているとする。
(1)\(\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\)の関係式を求めよ。
(2)\(\angle A\)の大きさを求めよ。

(解答)
(1)

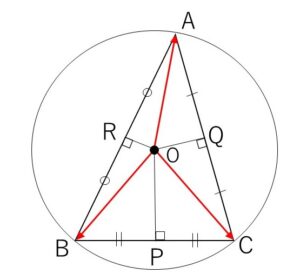
(注)図は鋭角三角形の場合 (直角三角形,鈍角三角形でも解答は同様になる)

\(P,Q,R\)は辺の中点となるから

\(\overrightarrow{OP}=\displaystyle\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})\)
\(\overrightarrow{OQ}=\displaystyle\frac{1}{2}(\overrightarrow{OC}+\overrightarrow{OA})\)
\(\overrightarrow{OR}=\displaystyle\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\)

これらを
\(\overrightarrow{OP}+2\overrightarrow{OQ}+3\overrightarrow{OR}=\vec{0}\)
に代入して

\(\displaystyle\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})+\displaystyle\frac{2}{2}(\overrightarrow{OC}+\overrightarrow{OA})+\displaystyle\frac{3}{2}(\overrightarrow{OA}+\overrightarrow{OB})=\vec{0}\)

したがって
\(5\overrightarrow{OA}+4\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}\)

(2)

(1)より
\(4\overrightarrow{OB}+3\overrightarrow{OC}=-5\overrightarrow{OA}\) だから
\(|4\overrightarrow{OB}+3\overrightarrow{OC}|^2=|-5\overrightarrow{OA}|^2\)
\(16|\overrightarrow{OB}|^2+24\overrightarrow{OB}\cdot\overrightarrow{OC}+9|\overrightarrow{OC}|^2=25|\overrightarrow{OA}|^2\)

\(|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|\) より

\(\overrightarrow{OB}\cdot\overrightarrow{OC}=0\)

よって \(\angle BOC=90°\)

ここで(1)の関係式から
\(\overrightarrow{OA}=-\displaystyle\frac{4\overrightarrow{OB}+3\overrightarrow{OC}}{5}\)
\(=-\displaystyle\frac{7}{5}\cdot\displaystyle\frac{4\overrightarrow{OB}+3\overrightarrow{OC}}{3+4}\)
\(=-\displaystyle\frac{7}{5}\overrightarrow{OD}\)

とすると、\(D\)は\(BC\)の内分点であり、点\(A\)の位置として\(\overrightarrow{OD}\)と同じ向きにある\(A’\)は不適となる。

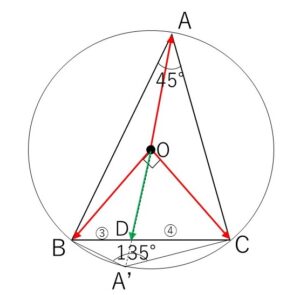
したがって
\(\angle A=90°÷2\)\(=45°\)

(別解)
\(\cos\angle A=\displaystyle\frac{\overrightarrow{AB}\cdot\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}\)

円の半径を\(r\)とする。

本解答と同じように
\(\overrightarrow{OB}\cdot\overrightarrow{OC}=0\)

他の内積も同様に
\(|5\overrightarrow{OA}+4\overrightarrow{OB}|^2=|-3\overrightarrow{OC}|^2\) から
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=-\displaystyle\frac{4}{5}r^2\)

\(|5\overrightarrow{OA}+3\overrightarrow{OC}|^2=|-4\overrightarrow{OB}|^2\) から
\(\overrightarrow{OC}\cdot\overrightarrow{OA}=-\displaystyle\frac{3}{5}r^2\)

よって
\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
\(=(\overrightarrow{OB}-\overrightarrow{OA})\cdot(\overrightarrow{OC}-\overrightarrow{OA})\)
\(=\overrightarrow{OB}\cdot\overrightarrow{OC}-\overrightarrow{OB}\cdot\overrightarrow{OA}-\overrightarrow{OA}\cdot\overrightarrow{OC}+|\overrightarrow{OA}|^2\)
\(=0+\displaystyle\frac{4}{5}r^2+\displaystyle\frac{3}{5}r^2+r^2\)
\(=\displaystyle\frac{12}{5}r^2\)

\(|\overrightarrow{AB}|^2\)
\(=|\overrightarrow{OB}-\overrightarrow{OA}|^2\)
\(=|\overrightarrow{OB}|^2-2\overrightarrow{OB}\cdot\overrightarrow{OA}+|\overrightarrow{OA}|^2\)
\(=r^2+\displaystyle\frac{8}{5}r^2+r^2\)
\(=\displaystyle\frac{18}{5}r^2\)

\(|\overrightarrow{AC}|^2\)
\(=|\overrightarrow{OC}-\overrightarrow{OA}|^2\)
\(=|\overrightarrow{OC}|^2-2\overrightarrow{OC}\cdot\overrightarrow{OA}+|\overrightarrow{OA}|^2\)
\(=r^2+\displaystyle\frac{6}{5}r^2+r^2\)
\(=\displaystyle\frac{16}{5}r^2\)

ゆえに
\(\cos\angle A=\displaystyle\frac{\overrightarrow{AB}\cdot\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}\)

\(=\displaystyle\frac{\displaystyle\frac{12}{5}r^2}{\sqrt{\displaystyle\frac{18}{5}}r\cdot\sqrt{\displaystyle\frac{16}{5}}r}\)

\(=\displaystyle\frac{1}{\sqrt{2}}\)

よって \(\angle A=45°\)

(例題2)
円に内接する四角形\(ABPC\)は次の条件(イ),(ロ)を満たすとする。
(イ)三角形\(ABC\)は正三角形である。
(ロ)\(AP\)と\(BC\)の交点は線分\(BC\)を \(p:1-p\)　(\(0<p<1\)) の比に内分する。
このときベクトル\(\overrightarrow{AP}\)を\(\overrightarrow{AB},\overrightarrow{AC},p\) を用いて表せ。

(解答)
(解法1)中心からの距離を考える方法

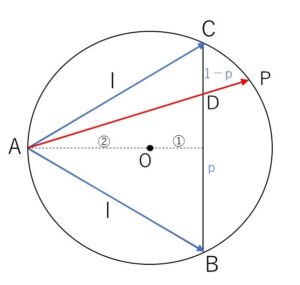
\(\overrightarrow{AB}=\vec{b}\), \(\overrightarrow{AC}=\vec{c}\) とし
円の中心を\(O\)、\(AP,BC\)の交点を\(D\)、正三角形の1辺の長さを\(l\)とする。

中心\(O\)と、三角形\(ABC\)の重心は一致するので
\(\overrightarrow{AO}=\displaystyle\frac{\vec{0}+\vec{b}+\vec{c}}{3}=\displaystyle\frac{\vec{b}+\vec{c}}{3}\)

(円の半径)\(=\displaystyle\frac{\sqrt{3}}{2}l×\displaystyle\frac{2}{3}=\displaystyle\frac{\sqrt{3}}{3}l\)

また
\(\overrightarrow{AP}=k\overrightarrow{AD}\)
\(=k\{(1-p)\vec{b}+p\vec{c}\}\)
と表せるので

\(\overrightarrow{OP}=\overrightarrow{AP}-\overrightarrow{AO}\)
\(=k\{(1-p)\vec{b}+p\vec{c}\}-\displaystyle\frac{\vec{b}+\vec{c}}{3}\)
\(=\{k(1-p)-\displaystyle\frac{1}{3}\}\vec{b}+(kp-\displaystyle\frac{1}{3})\vec{c}\)

\(P\)は円周上の点だから
\(|\overrightarrow{OP}|^2=(\displaystyle\frac{\sqrt{3}}{3}l)^2\)

ここで
\(|\vec{b}|=|\vec{c}|=l\)
\(\vec{b}\cdot\vec{c}=l^2\cos60°=\displaystyle\frac{1}{2}l^2\) であるから

\(\left|\{k(1-p)-\displaystyle\frac{1}{3}\}\vec{b}+(kp-\displaystyle\frac{1}{3})\vec{c}\right|^2=\displaystyle\frac{1}{3}l^2\)

\(\left\{k(1-p)-\displaystyle\frac{1}{3}\right\}^2l^2+2\{k(1-p)-\displaystyle\frac{1}{3}\}(kp-\displaystyle\frac{1}{3})\cdot\displaystyle\frac{1}{2}l^2+(kp-\displaystyle\frac{1}{3})^2l^2=\displaystyle\frac{1}{3}l^2\)

両辺\(l^2\)で割って、\(k\)の次数で分けて計算すると
\(k^2(p^2-p+1)-k=0\)
\(k\{k(p^2-p+1)-1\}=0\)

\(k=0\) とすると、\(A\)と\(P\)が一致するので内接四角形ができず不適。
よって
\(k=\displaystyle\frac{1}{p^2-p+1}\)

したがって
\(\overrightarrow{AP}=k\overrightarrow{AD}\)
\(=\displaystyle\frac{1}{p^2-p+1}\{(1-p)\overrightarrow{AB}+p\overrightarrow{AC}\}\)

(解法2)方べきの定理を使う方法

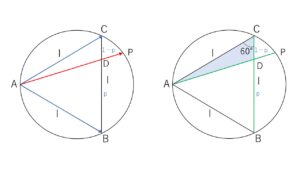
正三角形の1辺の長さ\(l\)とする。

条件より
\(BD=pl\),　\(DC=(1-p)l\)

また三角形\(ACD\)において余弦定理より
\(AD^2=l^2+(1-p)^2l^2-2l(1-p)l\cos60°\)
\(AD^2=l^2(p^2-p+1)\)
\(AD=l\sqrt{p^2-p+1}\)

方べきの定理から
\(AD×DP=BD×DC\)
\(DP=\displaystyle\frac{pl×(1-p)l}{l\sqrt{p^2-p+1}}=\displaystyle\frac{p(1-p)}{\sqrt{p^2-p+1}}l\)

よって
\(AP=(\sqrt{p^2-p+1}+\displaystyle\frac{p(1-p)}{\sqrt{p^2-p+1}})l\)

\(=\displaystyle\frac{1}{\sqrt{p^2-p+1}}l\) となるので

\(AP=\displaystyle\frac{1}{p^2-p+1}AD\)

したがって
\(\overrightarrow{AP}=\displaystyle\frac{1}{p^2-p+1}\overrightarrow{AD}\)

\(=\displaystyle\frac{1}{p^2-p+1}\{(1-p)\overrightarrow{AB}+p\overrightarrow{AC}\}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→点の一致　back→外接円・円周上の点とベクトル①