ベクトルと点の一致の問題です。
(例題1)
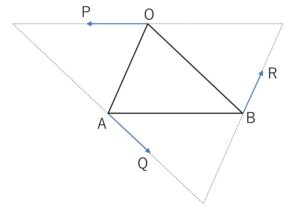
三角形\(OAB\)があり、3点\(P,Q,R\)を
\(\overrightarrow{OP}=k\overrightarrow{BA}\), \(\overrightarrow{AQ}=k\overrightarrow{OB}\), \(\overrightarrow{BR}=k\overrightarrow{AO}\)
となるように定める。ただし、\(k\)は \(0<k<1\) を満たす実数である。
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とおくとき
(1)\(\overrightarrow{OP},\overrightarrow{OQ},\overrightarrow{OR}\) をそれぞれ\(\vec{a},\vec{b},k\) を用いて表せ。
(2)三角形\(OAB\)の重心と三角形\(PQR\)の重心が一致することを示せ。
(解答)
(1)
\(\overrightarrow{OP}\)\(=k(\vec{a}-\vec{b})\)
\(\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{AQ}\)
\(=\vec{a}+k\vec{b}\)
\(\overrightarrow{OR}=\overrightarrow{OB}+\overrightarrow{BR}\)
\(=\vec{b}-k\vec{a}\)
(2)
\(△PQR\)の重心を\(G\)とすると
\(\overrightarrow{OG}=\displaystyle\frac{1}{3}(\overrightarrow{OP}+\overrightarrow{OQ}+\overrightarrow{OR})\)
\(=\displaystyle\frac{1}{3}\{k(\vec{a}-\vec{b})+(\vec{a}+k\vec{b})+(\vec{b}-k\vec{a})\}\)
\(=\displaystyle\frac{1}{3}(\vec{a}+\vec{b})\)
\(=\displaystyle\frac{1}{3}(\vec{0}+\vec{a}+\vec{b})\)
よって三角形\(OAB\)の重心と三角形\(PQR\)の重心は一致する。
(例題2)
正六角形\(OPQRST\)において、\(\overrightarrow{OP}=\vec{p}\), \(\overrightarrow{OQ}=\vec{q}\) とする。
(1)\(\overrightarrow{OR},\overrightarrow{OS},\overrightarrow{OT}\) を、それぞれ\(\vec{p},\vec{q}\) で表せ。
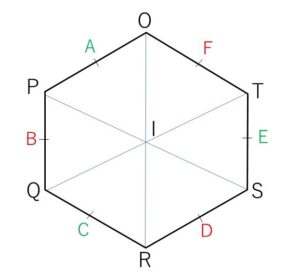
(2)\(△OQS\)の重心\(G_1\)と\(△PRT\)の重心\(G_2\)は一致することを証明せよ。また、辺\(OP,PQ,QR,RS,ST,TO\)の中点を、それぞれ\(A,B,C,D,E,F\)とするとき、\(△ACE\)の重心\(G_3\)、\(△BDF\)の重心\(G_4\)および\(G_1,G_2\)の4点は一致するか。
(解答)
(1)
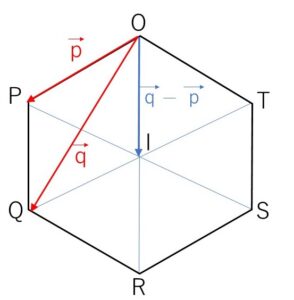
正六角形の対角線の交点を\(I\)とする。
\(\overrightarrow{OI}=\overrightarrow{PQ}=\vec{q}-\vec{p}\) より
\(\overrightarrow{OR}=2\overrightarrow{OI}\)\(=-2\vec{p}+2\vec{q}\)
\(\overrightarrow{OS}=\overrightarrow{OR}+\overrightarrow{RS}\)
\(=(-2\vec{p}+2\vec{q})+(-\vec{p})\)
\(=-3\vec{p}+2\vec{q}\)
\(\overrightarrow{OT}=\overrightarrow{OI}+\overrightarrow{IT}\)
\(=(-\vec{p}+\vec{q})+(-\vec{p})\)
\(=-2\vec{p}+\vec{q}\)
(2)
\(\overrightarrow{OG_1}\)
\(=\displaystyle\frac{1}{3}(\overrightarrow{OO}+\overrightarrow{OQ}+\overrightarrow{OS})\)
\(=\displaystyle\frac{1}{3}\{\vec{0}+\vec{q}+(-3\vec{p}+2\vec{q})\}\)
\(=-\vec{p}+\vec{q}\)
\(\overrightarrow{OG_2}\)
\(=\displaystyle\frac{1}{3}(\overrightarrow{OP}+\overrightarrow{OR}+\overrightarrow{OT})\)
\(=\displaystyle\frac{1}{3}\{\vec{p}+(-2\vec{p}+2\vec{q})+(-2\vec{p}+\vec{q})\}\)
\(=-\vec{p}+\vec{q}\)
よって \(G_1\)と\(G_2\)は一致する。
また
\(\overrightarrow{OG_3}\)
\(=\displaystyle\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OE})\)
\(=\displaystyle\frac{1}{3}(\displaystyle\frac{\overrightarrow{OP}}{2}+\displaystyle\frac{\overrightarrow{OQ}+\overrightarrow{OR}}{2}+\displaystyle\frac{\overrightarrow{OS}+\overrightarrow{OT}}{2})\)
\(=\displaystyle\frac{1}{6}(\overrightarrow{OP}+\overrightarrow{OQ}+\overrightarrow{OR}+\overrightarrow{OS}+\overrightarrow{OT})\)
\(=\displaystyle\frac{1}{6}\{\vec{p}+\vec{q}+(-2\vec{p}+2\vec{q})+(-3\vec{p}+2\vec{q})+(-2\vec{p}+\vec{q})\)
\(=-\vec{p}+\vec{q}\)
\(\overrightarrow{OG_4}\)
\(=\displaystyle\frac{1}{3}(\overrightarrow{OB}+\overrightarrow{OD}+\overrightarrow{OF})\)
\(=\displaystyle\frac{1}{3}(\displaystyle\frac{\overrightarrow{OP}+\overrightarrow{OQ}}{2}+\displaystyle\frac{\overrightarrow{OR}+\overrightarrow{OS}}{2}+\displaystyle\frac{\overrightarrow{OT}}{2})\)
\(=\displaystyle\frac{1}{6}(\overrightarrow{OP}+\overrightarrow{OQ}+\overrightarrow{OR}+\overrightarrow{OS}+\overrightarrow{OT})\)
\(=\overrightarrow{OG_3}\)
\(=-\vec{p}+\vec{q}\)
したがって4点\(G_1,G_2,G_3,G_4\)は一致する。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対称・回転とベクトル back→外接円・円周上の点とベクトル②