1次従属なベクトルと対称性(長方形・垂心)

平面においては2つの1次独立なベクトルを用意すれば、平面上の任意のベクトルはこの2つのベクトルを用いて表すことができます。大半の問題では2つの1次独立なベクトルを基本として扱っていきますが、中には複数のベクトルをそのままの状態で扱う場合もあります。こういったケースでは問題設定が対称性のある場合が多いです。

(例題1)
中心が\(O\)である定円の周上に相異なる6つの定点\(A_1,A_2,A_3,A_4,A_5,A_6\)がある。このとき、

(1)\(\overrightarrow{OA_1}+\overrightarrow{OA_2}+\overrightarrow{OA_3}=\overrightarrow{OH}\) となるように点\(H\)をとれば、点\(H\)は\(△A_1A_2A_3\)の垂心であることを示せ。
(2)6点\(A_k\) (\(k=1,2,3,4,5,6\)) のうちから3点を任意に選ぶ。選んだ3点を頂点とする三角形の垂心と、残りの3点を頂点とする三角形の重心とを通る直線は、3点の選び方に無関係な一定の点を通ることを示せ。

対称性のある問題設定です。誘導に沿っていけばあまり1次独立・従属は意識する必要がないかもしれませんが・・・。
なお\(OA_1～OA_6\) は半径ですべて等しいことはどこかで使うのでしょう。

(解答)
(1)

\(A_1H \perp A_2A_3\)などを示すために内積を計算していきます。

対称性ベクトル例題1

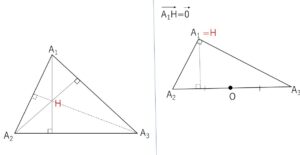
\(A_1\)～\(A_6\) は相異なる点であることに注意する。

\(\overrightarrow{A_1H}\cdot\overrightarrow{A_2A_3}\)
\(=(\overrightarrow{OH}-\overrightarrow{OA_1})\cdot(\overrightarrow{OA_3}-\overrightarrow{OA_2})\)
\(=(\overrightarrow{OA_3}+\overrightarrow{OA_2})\cdot(\overrightarrow{OA_3}-\overrightarrow{OA_2})\)
\(=|\overrightarrow{OA_3}|^2-|\overrightarrow{OA_2}|^2\)
\(=0\)

よって
\(\overrightarrow{A_1H} \perp \overrightarrow{A_2A_3}\) または \(\overrightarrow{A_1H}=\vec{0}\)

\(\overrightarrow{A_1H}=\vec{0}\) のとき (\(A_1\)と\(H\)が一致するとき)
条件式から
\(\overrightarrow{OA_2}+\overrightarrow{OA_3}=\overrightarrow{A_1H}=\vec{0}\)
したがって
\(\overrightarrow{OA_2}=-\overrightarrow{OA_3}\) となるので
\(A_2A_3\)は円の直径となる。
このとき、\(\angle A_1=90°\) となるから、\(H\) (\(A_1\)と一致) は垂心である。

\(\overrightarrow{A_1H}≠\vec{0}\) のとき、\(\overrightarrow{A_1H} \perp \overrightarrow{A_2A_3}\) であり
同様に、\(\overrightarrow{A_2H}\cdot\overrightarrow{A_3A_1}\) を計算すると、\(\overrightarrow{A_2H}\cdot\overrightarrow{A_3A_1}=0\) となるから
\(\overrightarrow{A_2H} \perp \overrightarrow{A_3A_1}\) または \(\overrightarrow{A_2H}=\vec{0}\)

\(\overrightarrow{A_2H}=\vec{0}\) のときは同様の議論により\(H\)は垂心。
\(\overrightarrow{A_2H}≠\vec{0}\) のときは \(\overrightarrow{A_2H} \perp \overrightarrow{A_3A_1}\) であるが、\(\overrightarrow{A_1H} \perp \overrightarrow{A_2A_3}\) と合わせると\(H\)が垂心となることが分かる。

以上より\(H\)は垂心である。

\(H≠A_1,A_2\)のとき、2頂点から垂線を下したときの交点\(H\)は垂心であることは保証されます(残りの1つの頂点から垂線を下せば\(H\)を通ります)。したがって、\(\overrightarrow{A_3H}\cdot\overrightarrow{A_1A_2}\) については考えなくもよいと思いますが、不安なら調べてもよいです。

(2)

選んだ3点を \(A_{k_1},A_{k_2},A_{k_3}\)、残りの3点を \(A_{k_4},A_{k_5},A_{k_6}\) とします。題意の直線上の点を\(P\)とすると
\(\overrightarrow{OP}=\overrightarrow{OA_{k_1}}+\overrightarrow{OA_{k_2}}+\overrightarrow{OA_{k_3}}\)
\(+k\left\{\displaystyle\frac{\overrightarrow{OA_{k_4}}+\overrightarrow{OA_{k_5}}+\overrightarrow{OA_{k_6}}}{3}-(\overrightarrow{OA_{k_1}}+\overrightarrow{OA_{k_2}}+\overrightarrow{OA_{k_3}})\right\}\)
3点の選び方によらずある定点\(P\)を通るということですが、それは\(\overrightarrow{OP}\)が対称な式になればよく、そうなるような\(k\)をうまく探します。\(\overrightarrow{OA_{k_1}},\overrightarrow{OA_{k_4}}\) の係数に着目して、\(1-k=\displaystyle\frac{1}{3}k\)。これを解くと \(k=\displaystyle\frac{3}{4}\) です。

選んだ3点を \(A_{k_1},A_{k_2},A_{k_3}\)、残りの3点を \(A_{k_4},A_{k_5},A_{k_6}\) とする。題意の直線上の点を\(P\)とすると
\(\overrightarrow{OP}=\overrightarrow{OA_{k_1}}+\overrightarrow{OA_{k_2}}+\overrightarrow{OA_{k_3}}\)
\(+k\left\{\displaystyle\frac{\overrightarrow{OA_{k_4}}+\overrightarrow{OA_{k_5}}+\overrightarrow{OA_{k_6}}}{3}-(\overrightarrow{OA_{k_1}}+\overrightarrow{OA_{k_2}}+\overrightarrow{OA_{k_3}})\right\}\)

ここで\(k=\displaystyle\frac{3}{4}\) とすると
\(\overrightarrow{OP}=\displaystyle\frac{1}{4}(\overrightarrow{OA_{k_1}}+\overrightarrow{OA_{k_2}}+\overrightarrow{OA_{k_3}}+\overrightarrow{OA_{k_4}}+\overrightarrow{OA_{k_5}}+\overrightarrow{OA_{k_6}})\)

(\(=\displaystyle\frac{1}{4}\overrightarrow{OS}\) とおく)

\(S\)は3点の選び方によらず定点になるので、題意の直線は3点の選び方に無関係な定点\(S\)を通る。

(例題2)
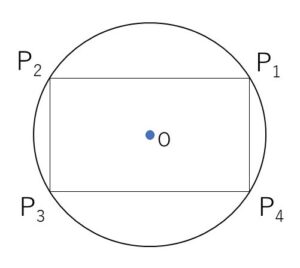
原点\(O\)を中心とする単位円周上に相異なる点\(P_1,P_2,P_3,P_4\) があって
\(\overrightarrow{OP_1}+\overrightarrow{OP_2}+\overrightarrow{OP_3}+\overrightarrow{OP_4}=\vec{0}\)
となっている。このとき、\(P_1,P_2,P_3,P_4\)はある長方形の頂点となることを示せ。

本問も対称性のある問題設定です。長方形の条件については次の通りです。
(1)4つの内角が\(90°\)
(2)平行四辺形 + 対角線の長さが等しい
(3)平行四辺形 + 1つの内角が\(90°\)
条件式より移項して2乗することで、さまざまな等しい内積の組が分かります。

(解答)
対称性により反時計回りに\(P_1,P_2,P_3,P_4\)の順に並ぶとしてよい。

対称性ベクトル例題2

与式から
\(|\overrightarrow{OP_1}+\overrightarrow{OP_2}|^2=|-(\overrightarrow{OP_3}+\overrightarrow{OP_4})|^2\)
\(|\overrightarrow{OP_1}|^2+2\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}+|\overrightarrow{OP_2}|^2=|\overrightarrow{OP_3}|^2+2\overrightarrow{OP_3}\cdot\overrightarrow{OP_4}+|\overrightarrow{OP_4}|^2\)

\(|\overrightarrow{OP_1}|=|\overrightarrow{OP_2}|=|\overrightarrow{OP_3}|=|\overrightarrow{OP_4}|=1\) より

\(\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}=\overrightarrow{OP_3}\cdot\overrightarrow{OP_4}\)・・・①

同様にして
\(\overrightarrow{OP_1}\cdot\overrightarrow{OP_3}=\overrightarrow{OP_2}\cdot\overrightarrow{OP_4}\)・・・②
\(\overrightarrow{OP_1}\cdot\overrightarrow{OP_4}=\overrightarrow{OP_2}\cdot\overrightarrow{OP_3}\)・・・③

ここで
\(|\overrightarrow{P_1P_2}|^2=|\overrightarrow{OP_2}-\overrightarrow{OP_1}|^2\)
\(=2-2\overrightarrow{OP_1}\cdot\overrightarrow{OP_2}\)
\(|\overrightarrow{P_3P_4}|^2=|\overrightarrow{OP_4}-\overrightarrow{OP_3}|^2\)
\(=2-2\overrightarrow{OP_3}\cdot\overrightarrow{OP_4}\)
①より
\(|\overrightarrow{P_1P_2}|=|\overrightarrow{P_3P_4}|\)

\(|\overrightarrow{P_2P_3}|^2=|\overrightarrow{OP_3}-\overrightarrow{OP_2}|^2\)
\(=2-2\overrightarrow{OP_2}\cdot\overrightarrow{OP_3}\)
\(|\overrightarrow{P_4P_1}|^2=|\overrightarrow{OP_1}-\overrightarrow{OP_4}|^2\)
\(=2-2\overrightarrow{OP_1}\cdot\overrightarrow{OP_4}\)
③より
\(|\overrightarrow{P_2P_3}|=|\overrightarrow{P_4P_1}|\)

したがって対辺がそれぞれ等しいので、四角形\(P_1P_2P_3P_4\)は平行四辺形。

また
\(|\overrightarrow{P_1P_3}|^2=|\overrightarrow{OP_3}-\overrightarrow{OP_1}|^2\)
\(=2-2\overrightarrow{OP_1}\cdot\overrightarrow{OP_3}\)
\(|\overrightarrow{P_2P_4}|^2=|\overrightarrow{OP_4}-\overrightarrow{OP_2}|^2\)
\(=2-2\overrightarrow{OP_2}\cdot\overrightarrow{OP_4}\)
②より
\(|\overrightarrow{P_1P_3}|=|\overrightarrow{P_2P_4}|\)

ゆえに対角線の長さが等しい。

以上より四角形\(P_1P_2P_3P_4\)は対角線の長さが等しい平行四辺形となるから、長方形である。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→チェバ,メネラウスの定理とベクトル