線分や三角形、平行四辺形の内部がベクトルによってどのように表されるか見ていきます。
・線分
\(A(\vec{a})\),\(B(\vec{b})\)において、直線\(AB\)上の点\(P(\vec{p})\)は
\(\vec{p}=s\vec{a}+t\vec{b}\), \(s+t=1\) ・・・①
と表されましたが、\(t\)や\(s\)の値によって\(P\)がどの位置にあるかを検討してみます。基準を\(O\)として①を改めて
\(\vec{p}=(1-t)\vec{a}+t\vec{b}\)
\(=\vec{a}+t(\vec{b}-\vec{a})\)
\(=\overrightarrow{OA}+t\overrightarrow{AB}\)
と表すと、\(A\)から\(P\)がどれくらい離れているかは\(t\)によって決まるので、\(t\)の値による\(P\)の位置は次のようになります。
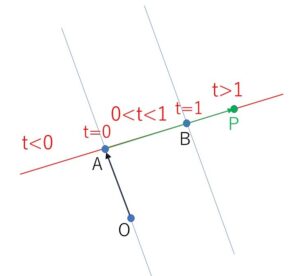
よって、\(P\)が線分\(AB\)上にある(\(A,B\)も含む)とき
\(\vec{p}=s\vec{a}+t\vec{b}\), \(s+t=1\), \(0≦t≦1\)
となりますが、\(t≦1\) の部分を
\(t=1-s≦1\) つまり \(s≧0\)
とすれば、線分\(AB\)を表すベクトル方程式は次の通りです。
\(\vec{p}=s\vec{a}+t\vec{b}\), \(s+t=1\), \(s≧0\), \(t≧0\)
以下 \(\vec{a},\vec{b}\) は1次独立とします。
・三角形の周および内部
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OP}=\vec{p}\) とし
線分のベクトル方程式を利用すると、三角形\(OAB\)の周および内部を表すベクトル方程式は次の通りです。
\(\vec{p}=s\vec{a}+t\vec{b}\), \(0≦s+t≦1\), \(s≧0\), \(t≧0\)
(解説)
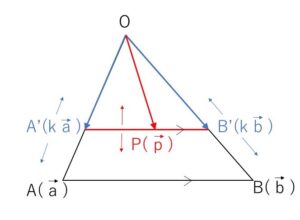
(1)\(s+t=k\) (\(0<k≦1\)) とおく。
\(k≠0\)より \(\displaystyle\frac{s}{k}+\displaystyle\frac{t}{k}=1\)
\(\vec{p}=s\vec{a}+t\vec{b}\)
\(=\displaystyle\frac{s}{k}(k\vec{a})+\displaystyle\frac{t}{k}(k\vec{b})\)
ここで \(A'(k\vec{a})\), \(B'(k\vec{b})\) とおくと、\(0<k≦1\) より \(A’,B’\)はそれぞれ線分\(OA,OB\)上(\(O\)を除く)の点で、同じ比により線分\(A’B’\)は\(AB\)に平行になる。
また、 \(\displaystyle\frac{s}{k}+\displaystyle\frac{t}{k}=1\), \(\displaystyle\frac{s}{k}≧0\), \(\displaystyle\frac{t}{k}≧0\) の3つの条件を満たすので、\(P\)は\(AB\)に平行な線分\(A’B’\)上(\(A’,B’\)を含む)を動くことになる。
そして \(0<k≦1\) の範囲で\(k\)が動くと、\(A’,B’\)はそれぞれ線分\(OA,OB\)上(\(O\)を除く)を動くので、\(P\)は\(O\)を除く三角形\(OAB\)の周および内部を動くことになる。
(2)\(s+t=0\) のとき
\(s≧0\), \(t≧0\) より、\(s=t=0\)
このとき \(P\)は\(O\)と一致する。
以上より\(P\)は三角形\(OAB\)の周および内部を動くことになる。
・平行四辺形の周および内部
\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(\overrightarrow{OC}=\vec{a}+\vec{b}\), \(\overrightarrow{OP}=\vec{p}\) とすると
平行四辺形\(OABC\)の周および内部のベクトル方程式は次の通りです。
\(\vec{p}=s\vec{a}+t\vec{b}\), \(0≦s≦1\), \(0≦t≦1\)
(解説)
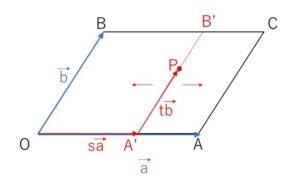
まず、\(s\)を固定する。
\(A'(s\vec{a})\) (固定点)とおくと
\(\vec{p}=s\vec{a}+t\vec{b}\)\(=s\overrightarrow{OA’}+t\vec{b}\)
より、\(0≦t≦1\)で動かすと\(P\)は図の線分\(A’B’\)上を動く。
次に\(s\)を \(0≦s≦1\) で動かすと、線分\(A’B’\)は線分\(OB\)から線分\(AC\) まで平行に動く。
したがって、点\(P\)は平行四辺形の周および内部を動くことになる。
今回の内容の演習は次回に回したいと思います。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡・領域②(線分・三角形,平行四辺形の内部) back→円の接線の方程式