座標を利用するベクトルの軌跡・領域の問題についてみていきます。
(例題1)
座標平面上で、原点\(O\)を基準とする点\(P\)の位置ベクトル\(\overrightarrow{OP}\)が\(\vec{p}\)であるとき、点\(P\)を\(P(\vec{p})\)で表す。
(1)\(A(\vec{a})\)を原点\(O\)と異なる点とする。
(i)点\(A(\vec{a})\)を通り、ベクトル\(\vec{a}\)に垂直な直線上の任意の点を\(P(\vec{p})\)とするとき、\(\vec{a}\cdot\vec{p}=|\vec{a}|^2\) が成り立つことを示せ。
(ii)ベクトル方程式 \(|\vec{p}|^2-2\vec{a}\cdot\vec{p}=0\) で表される図形を図示せよ。
(2)ベクトル \(\vec{b}=(1,1)\) に対して、不等式
\(|\vec{p}-\vec{b}|≦|\vec{p}+3\vec{b}|≦3|\vec{p}-\vec{b}|\)
を満たす点\(P(\vec{p})\)全体が表す領域を図示せよ。
(解答)
(1)
(i)
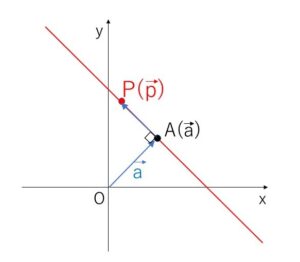
\(\overrightarrow{OA} \perp \overrightarrow{AP}\) または \(\overrightarrow{AP}=\vec{0}\) より
\(\overrightarrow{OA}\cdot\overrightarrow{AP}=0\)
よって
\(\vec{a}\cdot(\vec{p}-\vec{a})=0\)
\(\vec{a}\cdot\vec{p}=|\vec{a}|^2\)
(ii)
\(|\vec{p}|^2-2\vec{a}\cdot\vec{p}=0\) より
\(|\vec{p}|^2-2\vec{a}\cdot\vec{p}+|\vec{a}|^2-|\vec{a}|^2=0\)
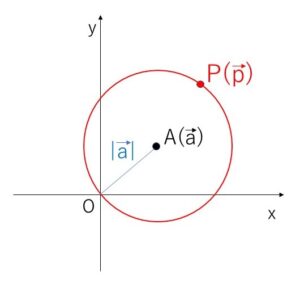
\(|\vec{p}-\vec{a}|^2=|\vec{a}|^2\)・・・①
①は中心\(A\)、半径\(|\vec{a}|\)の円を表している。
この円は原点を通るから図示すると次の通り。
(2)
\(\vec{p}=(x,y)\) とおく。
\(|\vec{p}-\vec{b}|≦|\vec{p}+3\vec{b}|≦3|\vec{p}-\vec{b}|\)
\(\vec{b}=(1,1)\) より
(ア)不等式の左辺と中辺
\(|\vec{p}-\vec{b}|≦|\vec{p}+3\vec{b}|\) について
\(|\vec{p}-\vec{b}|^2≦|\vec{p}+3\vec{b}|^2\)
\(\vec{p}-\vec{b}=(x-1,y-1)\), \(\vec{p}+3\vec{b}=(x+3,y+3)\) だから
\((x-1)^2+(y-1)^2≦(x+3)^2+(y+3)^2\)
整理すると
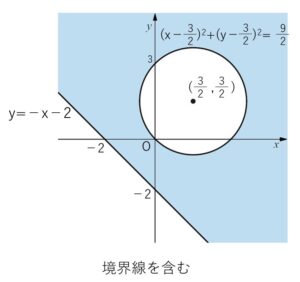
\(y≧-x-2\)・・・②
(イ)不等式の中辺と右辺
\(|\vec{p}+3\vec{b}|≦3|\vec{p}-\vec{b}|\) について
\(|\vec{p}+3\vec{b}|^2≦9|\vec{p}-\vec{b}|^2\)
\(\vec{p}+3\vec{b}=(x+3,y+3)\), \(\vec{p}-\vec{b}=(x-1,y-1)\) だから
\((x+3)^2+(y+3)^2≦9\{(x-1)^2+(y-1)^2\}\)
整理すると
\(x^2-3x+y^2-3y≧0\)
\((x-\displaystyle\frac{3}{2})^2+(y-\displaystyle\frac{3}{2})^2≧\displaystyle\frac{9}{2}\)・・・③
②かつ③が表す領域が求めるもので、図示すると次の通り。
(例題2)
平面上のベクトル \(\vec{a},\vec{b}\) が
\(|\vec{a}|=|\vec{b}|=1\), \(\vec{a}\cdot\vec{b}=-\displaystyle\frac{1}{2}\)
を満たすとする。
(1)実数\(p,q\)に対して、\(\vec{c}=p\vec{a}+q\vec{b}\) とおく。このとき、次の条件 \(|\vec{c}|=1\), \(\vec{a}\cdot\vec{c}=0\), \(p>0\) を満たす実数\(p,q\)を求めよ。
(2)平面上のベクトル\(\vec{x}\)が \(-1≦\vec{a}\cdot\vec{x}≦1\), \(1≦\vec{b}\cdot\vec{x}≦2\) を満たすとき、\(|\vec{x}|\)のとりうる値の範囲を求めよ。
(解答)
(1)
\(|\vec{c}|^2=1^2\) より
\(|p\vec{a}+q\vec{b}|^2=1\)
\(p^2-pq+q^2=1\)・・・①
\(\vec{a}\cdot\vec{c}=0\) より
\(\vec{a}(p\vec{a}+q\vec{b})=0\)
\(p-\displaystyle\frac{1}{2}q=0\)・・・②
②より \(q=2p\)・・・③ を①に代入して
\(p^2-2p^2+4p^2=1\)
\(p^2=\displaystyle\frac{1}{3}\)
\(p>0\)より
\(p=\displaystyle\frac{1}{\sqrt{3}}\)
③より
\(q=\displaystyle\frac{2}{\sqrt{3}}\)
(2)
\(|\vec{x}|^2=s^2-st+t^2\)
残りの2つの不等式は直線で囲まれる領域になるので、\(s^2-st+t^2=k\)・・・(i) とおいたときの共有点をもつときを考えることになりますが、(i)はよく分からない図形です(実は傾いた楕円です)。
そこで(1)の\(\vec{c}\)を使って、\(\vec{x}\)を \(\vec{a},\vec{c}\) (1次独立でしかも垂直) を使って、\(\vec{x}=s\vec{a}+t\vec{c}\) とすると
\(|\vec{x}|=s^2+t^2\)
となるので、\(s^2+t^2=k\) とおいたときに円になるのでこれなら大丈夫そうです。
もしくは、\(\vec{x},\vec{a},\vec{b}\)を成分表示する方法もあります(解答の中身はほとんど一緒なので別解で簡単に紹介します)。
\(\vec{a},\vec{c}\)は1次独立だから
\(\vec{x}=s\vec{a}+t\vec{c}\) (\(s,t\)は実数)とおける。
\(-1≦\vec{a}\cdot\vec{x}≦1\) より
\(-1≦\vec{a}\cdot(s\vec{a}+t\vec{c})≦1\)
\(-1≦s≦1\)・・・④
\(1≦\vec{b}\cdot\vec{x}≦2\) より
\(1≦\vec{b}\cdot(s\vec{a}+t\vec{c})≦2\)
\(1≦-\displaystyle\frac{1}{2}s+t\vec{b}\cdot\vec{c}≦2\)
ここで
\(\vec{b}\cdot\vec{c}\)
\(=\vec{b}\cdot(\displaystyle\frac{1}{\sqrt{3}}\vec{a}+\displaystyle\frac{2}{\sqrt{3}}\vec{b})\)
\(=-\displaystyle\frac{1}{2\sqrt{3}}+\displaystyle\frac{2}{\sqrt{3}}\)
\(=\displaystyle\frac{\sqrt{3}}{2}\) だから
\(1≦-\displaystyle\frac{1}{2}s+\displaystyle\frac{\sqrt{3}}{2}t≦2\)
\(\displaystyle\frac{1}{\sqrt{3}}s+\displaystyle\frac{2}{\sqrt{3}}≦t≦\displaystyle\frac{1}{\sqrt{3}}s+\displaystyle\frac{4}{\sqrt{3}}\)・・・⑤
ここで \(|\vec{x}|^2=|s\vec{a}+t\vec{c}|^2=s^2+t^2\) より
\(s,t\)平面上に④⑤で表される領域を図示して
\(s^2+t^2=k\) (\(k≧0\))
が④⑤の領域と共有点をもつときの\(k\)の範囲を求めればよい。
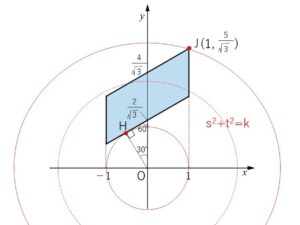
最小値をとるときは \((s,t)\) が図の\(H\)の座標のときで、\(k\)の最小値は
\(OH=\displaystyle\frac{2}{\sqrt{3}}\cos30°=\)\(1\)
最大値をとるときは \((s,t)\) が図の\(J\)の座標のときで、\(k\)の最大値は
\(s^2+t^2=1^2+(\displaystyle\frac{5}{\sqrt{3}})^2=\)\(\displaystyle\frac{28}{3}\)
したがって
\(1≦|\vec{x}|^2≦\displaystyle\frac{28}{3}\)
\(1≦|\vec{x}|≦\displaystyle\frac{2\sqrt{21}}{3}\)
(別解)
\(\vec{x}=(s,t)\) とおくのよいとして\(\vec{a},\vec{b}\)のおきかたですが、なす角\(120°\)の大きさ\(1\)のベクトルであることから、\(\vec{a}\)と重なるように\(x\)軸の正方向を設定すれば、\(\vec{a}=(1,0)\), \(\vec{b}=(\cos120°,\sin120°)\) です。(\(\vec{b}=(\cos(-120°),\sin(-120°))\) も考えられますが、この場合でも\(y\)軸を逆方向に設定すれば同じことになる)
\(\vec{x}=(s,t)\), \(\vec{a}=(1,0)\), \(\vec{b}=(-\displaystyle\frac{1}{2},\displaystyle\frac{\sqrt{3}}{2})\) と設定すると
\(|\vec{x}|^2=s^2+t^2\)
\(-1≦\vec{a}\cdot\vec{x}≦1\) より
\(-1≦s≦1\)・・・④
\(1≦\vec{b}\cdot\vec{x}≦2\) より
\(1≦-\displaystyle\frac{1}{2}s+\displaystyle\frac{\sqrt{3}}{2}t≦2\)
\(\displaystyle\frac{1}{\sqrt{3}}s+\displaystyle\frac{2}{\sqrt{3}}≦t≦\displaystyle\frac{1}{\sqrt{3}}s+\displaystyle\frac{4}{\sqrt{3}}\)・・・⑤
と先ほどの解答と全く同じ式となります。
実は・・・
\(\vec{c}\)が\(\vec{a}\)に垂直なので、\(\vec{c}=(0,1)\) or \((0,-1)\)。
(1)より\(\vec{c}\)を計算してみると
\(\vec{c}=\displaystyle\frac{1}{\sqrt{3}}(1,0)+\displaystyle\frac{2}{\sqrt{3}}(-\displaystyle\frac{1}{2},\displaystyle\frac{\sqrt{3}}{2})=(0,1)\)
と\(y\)成分が正のものになります。
すると
\(\vec{x}=(s,t)=s(1,0)+t(0,1)=s\vec{a}+t\vec{c}\)
となるので、この成分表示の解法は、\(\vec{x}=s\vec{a}+t\vec{c}\) とおく解法と本質的には同じになるわけです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→領域・軌跡④(等式・幾何の利用) back→領域・軌跡②(線分・三角形,平行四辺形の内部)