逆関数を求める問題について見ていきます。
(例題1)
次の関数の逆関数を求めよ。
(1)\(y=\displaystyle\frac{2x+8}{x+1}\) (\(0≦x≦2\))
(2)\(y=3^x-2\) (\(x\)は実数全体)
(解答)
(1)
\(y=\displaystyle\frac{2x+8}{x+1}\)
\(=\displaystyle\frac{2(x+1)+6}{x+1}\)
\(=\displaystyle\frac{6}{x+1}+2\)・・・①
よって \(0≦x≦2\) での値域は \(\displaystyle\frac{6}{2+1}+2≦y≦\displaystyle\frac{6}{0+1}+2\) より
\(4≦y≦8\)
よって逆関数の定義域は \(4≦x≦8\) で①において\(x,y\)を入れ替えて
\(x=\displaystyle\frac{6}{y+1}+2\)
\(x-2=\displaystyle\frac{6}{y+1}\)
\(\displaystyle\frac{1}{x-2}=\displaystyle\frac{y+1}{6}\)
ゆえに逆関数は
\(y=\displaystyle\frac{6}{x-2}-1\) (\(4≦x≦8\))
(2)
\(y=3^x-2\)・・・② (指数関数)の値域は
\(y≧-2\)
よって逆関数の定義域は \(x≧-2\) で、②で\(x,y\)を入れ替えると
\(x=3^y-2\)
\(3^y=x+2\)
底を\(3\)とする対数をとって
\(y=\log_{3}(x+2)\) (\(x≧-2\))
(例題2)
関数 \(f(x)=2x^2+2x+1\) (\(x≧-\displaystyle\frac{1}{2}\)) の逆関数を\(g(x)\)とする。
(1)関数\(g(x)\)の定義域を求めよ。
(2)\(g(x)\)を求めよ。
(3)曲線 \(y=g(x)\) 上の点と直線 \(y=2x-1\) の距離の最小値と、その最小値を与える \(y=g(x)\) 上の点をそれぞれ求めよ。
(解答)
(1)
\(f(x)=2(x+\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{2}\)
\(x≧-\displaystyle\frac{1}{2}\) より \(f(x)≧\displaystyle\frac{1}{2}\)
よって\(g(x)\)の定義域は
\(x≧\displaystyle\frac{1}{2}\)
(2)
\(y=2x^2+2x+1\) (\(x≧-\displaystyle\frac{1}{2}\))
の\(x,y\)を入れ替えると
\(x=2y^2+2y+1\) (\(y≧-\displaystyle\frac{1}{2}\))
よって
\(2y^2+2y+1-x=0\)
\(y=\displaystyle\frac{-1±\sqrt{1^2-2(1-x)}}{2}\)
\(=-\displaystyle\frac{1}{2}±\displaystyle\frac{1}{2}\sqrt{2x-1}\)
((1)より\(2x-1≧0\))
ここで \(y≧-\displaystyle\frac{1}{2}\) より根号が負になるほうは不適。よって逆関数は
\(g(x)=-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}\sqrt{2x-1}\)
(3)
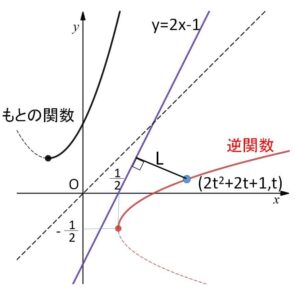
\(y=g(x)\) 上の点は
\((2t^2+2t+1,t)\) (\(t≧-\displaystyle\frac{1}{2}\))
とおける。この点と \(2x-y-1=0\) との距離\(L\)は
\(L=\displaystyle\frac{|2(2t^2+2t+1)-t-1|}{\sqrt{2^2+1}}\)
\(=\displaystyle\frac{1}{\sqrt{5}}|4t^2+3t+1|\)
\(=\displaystyle\frac{1}{\sqrt{5}}|4(t+\displaystyle\frac{3}{8})^2+\displaystyle\frac{7}{16}|\)
よって \(t≧-\displaystyle\frac{1}{2}\) において\(L\)が最小となるのは
\(t=-\displaystyle\frac{3}{8}\) のとき。このとき最小値は
\(L=\displaystyle\frac{7}{16\sqrt{5}}\)
で、最小値を与える\(y=g(x)\) 上の点は
\((2(-\displaystyle\frac{3}{8})^2+2(-\displaystyle\frac{3}{8})+1,-\displaystyle\frac{3}{8})\)
\(=(\displaystyle\frac{17}{32},-\displaystyle\frac{3}{8})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→逆関数ともとの関数の一致 back→逆関数の性質とグラフ