逆関数ともとの関数の交点に関する例題です。
(例題1)
2つの関数を
\(f(x)=\sqrt{x+4}\) (\(x≧-4\))
\(g(x)=x^2-4\) (\(x≧0\))
とし、\(y=f(x)\), \(y=g(x)\) で表される曲線をそれぞれ\(C_1,C_2\)とする。
(1)\(f(x)\)の逆関数が\(g(x)\)であることを示せ。
(2)曲線\(C_1\)と曲線\(C_2\)の交点\(P\)の座標を求めよ。
(解答)
(1)
\(y=\sqrt{x+4}\)・・・① (\(x≧-4\)) について
\(y≧0\)・・・②
①を2乗して
\(y^2=x+4\)
\(x=y^2-4\)
\(x,y\)を入れ替えると
\(y=x^2-4\)
よって
\(g(x)=x^2-4\)
定義域は②から\(x≧0\)
(2)
そこで、2つの関数のグラフが \(y=x\) に対称なことに着目してグラフをかくと、交点が \(y=x\) 上にあり、それ以外にはないことが分かります。ここで注意してほしいのが、\(y=x\)上をもとの関数\(y=f(x)\)が通過すれば、逆関数もその点を通るから交点になりますが、\(y=f(x)\)自身に\(y=x\)について対称な点がある場合には、その点も逆関数との交点となり、\(y=x\) 上にない場合があります。グラフで判断する場合にはそこを断っておいてください。(詳しくは次回に例題を扱います)
なお、別解では式変形で解く方法(4次方程式を避ける方法)もやっておきます。
\(C_1,C_2\)のグラフは次の通り。
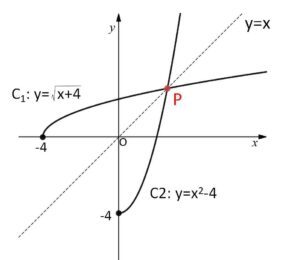
交点はただ1つで\(y=x\)上にあるから
\(y=x\)
\(y=x^2-4\) (曲線\(C_2\))
より\(y\)を消去すると
\(x=x^2-4\)
\(x^2-x-4=0\)
\(x=\displaystyle\frac{1±\sqrt{17}}{2}\)
\(x≧0\) より、交点\(P\)の座標は
\((\displaystyle\frac{1+\sqrt{17}}{2},\displaystyle\frac{1+\sqrt{17}}{2})\)
(別解)
\(x=y^2-4\)・・・(i) (\(y≧0\))
\(y=x^2-4\)・・・(ii) (\(x≧0\))
(同値性を意識すると)
「(i)かつ(ii)」 \(⇔\) 「(i)+(ii) かつ (i)-(ii)」
\(x+y=x^2+y^2-8\)・・・(iii)
\(x-y=y^2-x^2\)・・・(iv)
(\(x,y≧0\))
(iv)より
\((x-y)(x+y+1)=0\)
(ア)\(x=y\)のとき
(iii)に代入して ((i)や(ii)に代入してもよい)
\(2x=x^2+x^2-8\)
\(x^2-x-4=0\)
\(x=\displaystyle\frac{1±\sqrt{17}}{2}\)
\(x≧0\) を満たすのは
\(x=\displaystyle\frac{1+\sqrt{17}}{2}\)
このとき、\(y=\displaystyle\frac{1+\sqrt{17}}{2}\ (≧0)\)
(イ)\(x+y+1=0\) のとき
(iii)に代入して
\(-1=x^2+(-x-1)^2-8\)
整理して
\(x^2+x-3=0\)
\(x=\displaystyle\frac{-1±\sqrt{13}}{2}\)
\(x≧0\) より
\(x=\displaystyle\frac{-1+\sqrt{13}}{2}\) であるが
\(y=-x-1=\displaystyle\frac{-1-\sqrt{13}}{2}<0\) より不適。
(そもそも \(x+y+1=0\) で\(x,y\)が同時に\(0\)以上になることはない)
参考として定義域を制限しない場合のグラフをかくと次の通りです。
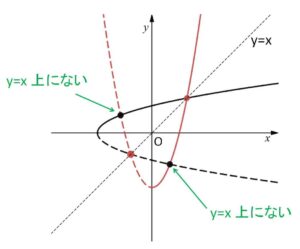
\(y=x\) 上にあるもう1つの交点は、(ア)で捨てた \(x=\displaystyle\frac{1-\sqrt{17}}{2}\ (=y)\) です。
(例題2)
\(a>0\)とし、\(f(x)=\sqrt{ax-2}-1\) (\(x≧\displaystyle\frac{2}{a}\)) とする。
(1)関数 \(y=f(x)\) の逆関数 \(y=f^{-1}(x)\) を求めよ。
(2)曲線 \(C_1:y=f(x)\) と 曲線 \(C_2:y=f^{-1}(x)\) が異なる2点で交わるとする。
(i)\(a\)のとり得る値の範囲を求めよ。
(ii)\(C_1\)と\(C_2\)の交点の\(x\)座標の差が\(2\)であるとする。このとき、\(a\)の値および\(C_1\)と\(C_2\)とで囲まれる図形の面積を求めよ。
(解答)
(1)
\(y=\sqrt{ax-2}-1\)・・・① の値域は
\(y≧-1\)
また①より
\(y+1=\sqrt{ax-2}\)
\((y+1)^2=ax-2\)
よって
\(x=\displaystyle\frac{1}{a}\{(y+1)^2+2\}\) (\(y≧-1\))
\(x,y\)を入れ替えることで逆関数が得られる。
\(f^{-1}(x)=\displaystyle\frac{1}{a}\{(x+1)^2+2\}\) (\(x≧-1\))
(2)
(i)
今回も、グラフの形状から \(y=x\)上 以外には交点がないことは断っておきます。
また、別解として数式処理の方法もやっておきます。こちらのほうだと \(y=x\) 上のみに交点があることがはっきりと分かります。
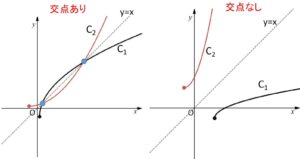
\(C_1,C_2\)のグラフは図のように\(y=x\)について対称でその交点は\(y=x\)上にある。
よって、\(C_2\)と\(y=x\)が異なる2点で交わる条件を考えると、方程式
\(x=\displaystyle\frac{1}{a}\{(x+1)^2+2\}\)・・・②
が、\(x≧-1\) で異なる2つの実数解をもてばよい。
②を整理すると
\(x^2+(2-a)x+3=0\)
(ア)判別式 \(D>0\)
(イ)軸 \(\displaystyle\frac{a-2}{2}>-1\)
(ウ)端点 \((-1)^2-(2-a)+3≧0\)
(ア)
\(D=(2-a)^2-12>0\)
\(a^2-4a-8>0\)
\(a<2-2\sqrt{3}\), \(a>2+2\sqrt{3}\)
(イ)
\(a-2>-2\)
\(a>0\)
(ウ)
\(2+a≧0\)
\(a≧-2\)
共通部分をとって
\(a>2+2\sqrt{3}\)
(別解)
\(C_2:\) \(y=\displaystyle\frac{1}{a}\{(x+1)^2+2\}\) (\(x≧-1\))・・・(A)
\(C_1:\) \(x=\displaystyle\frac{1}{a}\{(y+1)^2+2\}\) (\(y≧-1\))・・・(B)
(A)-(B) より
\(y-x=\displaystyle\frac{1}{a}\{(x+1)^2-(y+1)^2\}\)
\(a(y-x)=(x+y+2)(x-y)\)
\((x+y+2+a)(x-y)=0\)
ここで、\(x,y≧-1\), \(a>0\) より
\(x+y+2+a>0\) となるから
\(x-y=0\)
つまり \(x=y\)
あとは(A)か(B)にこれを代入すれば本解答と同様に2次式が得られる。
(ii)
面積については、積分です。直接2曲線の方程式の差をとる方法だと無理関数の積分(数Ⅲ)が必要です。
しかし、\(y=x\) について図形が対称であることを利用して半分の部分の面積を求めると、整式の積分になりしかも\(\displaystyle\frac{1}{6}\)公式が利用できます。
(i)より
\(x^2+(2-a)x+3=0\)
の2解の差が\(2\)であればよいから
\(\sqrt{D}=\sqrt{a^2-4a-8}=2\)
\(a^2-4a-8=4\)
\(a^2-4a-12=0\)
\((a-6)(a+2)=0\)
\(a>2+2\sqrt{3}\) を満たすのは
\(a=6\)
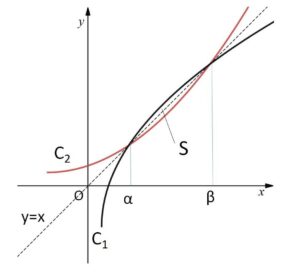
また、囲まれた図形は\(y=x\)について対称だからその面積\(S\)は、2交点の\(x\)座標を\(α,β\) (\(α<β\)) とすると、\(β-α=2\) であり
\(S=2\displaystyle\int_{α}^{β}[x-\displaystyle\frac{1}{6}\{(x+1)^2+2\}]dx\)
\(=(-\displaystyle\frac{1}{3})\displaystyle\int_{α}^{β}(x-α)(x-β)dx\)
\(=(-\displaystyle\frac{1}{3})\{\displaystyle\frac{-(β-α)^3}{6}\}\)
\(=\displaystyle\frac{2^3}{18}\)
\(=\displaystyle\frac{4}{9}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→逆関数ともとの関数の共有点② (y=x 上にない点) back→逆関数ともとの関数の一致