最大最小の数と確率 | 教えて数学理科

サイコロを何回か投げて、出る目の最大値最小値に関する確率の問題について見ていきます。

(例題)
さいころを\(n\)回 (\(n≧2\))投げるとき、次の確率を求めよ。
(1)出る目がすべて5以下である確率
(2)出る目の最大値が5である確率
(3)出る目の最小値が3である確率
(4)出る目の最小値が2で、かつ最大値が4である確率

(解答)
(1)
1から5までの目だけが出ればよいので、
\((\displaystyle\frac{5}{6})^n\)

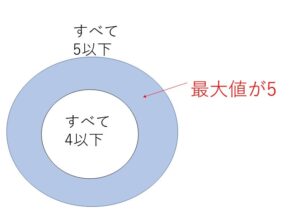
(2)

(1)を利用します。
(1)ではすべての目が5以下ですが、そのうち最大値が5にならない場合は、1から4までの目しか出ない場合です。(1)からこの場合を除いてあげましょう。

最大値が5となるのは、(1)の中で1から4までの目しか出ない場合でないときなので、
\((\displaystyle\frac{5}{6})^n-(\displaystyle\frac{4}{6})^n=\)\((\displaystyle\frac{5}{6})^n-(\displaystyle\frac{2}{3})^n\)

図で表すと次の通りです。余事象の確率と同様の考え方です。

(3)

(2)と同じように考えます。3以上の目のみがでる確率から、4以上の目のみがでる確率を除きます。

最小値が3となるのは、3から6までの目のみが出る場合のなかで、4から6までの目のみが出る場合でないときなので

\((\displaystyle\frac{4}{6})^n-(\displaystyle\frac{3}{6})^n=\)\((\displaystyle\frac{2}{3})^n-(\displaystyle\frac{1}{2})^n\)

(4)

最小値が2で最大値が4であることから、2,3,4の目しかでない場合を考えることになります。以下2,3,4の目のみで話を進めます。
また、条件は言い換えると「少なくとも2が1回出る　かつ　少なくとも4が1回出る」ことになります。
事象X「2,3,4のいずれかの目しか出ない」
事象A「少なくとも2が1回出る」
事象B「少なくとも4が1回でる」
として、求める確率は、余事象の確率の考え方を利用すると
\(P(A \cap B)=P(X)-P(\overline {A \cap B})\)
\(=P(X)-P(\overline A \cup \overline B)\)
\(=P(X)-\{P(\overline A)+P(\overline B)-P(\overline A \cap \overline B)\}\)
となります。

条件より、2,3,4の目しか出ない場合を考える。
以下2,3,4の目のみついて考える。

事象X「2,3,4のいずれかの目しかでない」
事象A「少なくとも2が1回出る」
事象B「少なくとも4が1回でる」

とすると、

\(P(A \cap B)=P(X)-P(\overline {A \cap B})\)
\(=P(X)-P(\overline A \cup \overline B)\)
\(=P(X)-\{P(\overline A)+P(\overline B)-P(\overline A \cap \overline B)\}\)

事象\(\overline A\)は「3,4の目しか出ない」
事象\(\overline B\)は「2,3の目しか出ない」
となるので、求める確率は

\(P(A \cap B)=(\displaystyle\frac{3}{6})^n-\)\(\{(\displaystyle\frac{2}{6})^n+(\displaystyle\frac{2}{6})^n-(\displaystyle\frac{1}{6})^n\}\)
\(=\)\((\displaystyle\frac{1}{2})^n-2(\displaystyle\frac{1}{3})^n+(\displaystyle\frac{1}{6})^n\)

結局は、「2,3,4の目が出る」場合から、「4が出ない」「2が出ない」場合を除いて、「4が出ないかつ2が出ない(つまり、3のみが出る)」を2回除いているので、この分を調整として1回足していることになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→1点の移動と反復試行　 next→対戦ゲームと確率