反射に関する例題です。対称移動させることがポイントになります。
・反射と対称移動

ある箱の中で直進し壁に反射する光線の進路を考えます。反射する際には入射角と反射角が等しくなるように反射をし、箱の中を繰り返し反射しながら光線は進みますが、そのままの進路を考えるのは大変です。そこで反射する際に光線が直進すると考えると、対頂角が等しいことから図の●同士と×同士の角度が等しくになり、直進光の進路は反射光の進路と反射面に関して対称になります。そこで箱を対称移動(線対称移動)させて格子を作ることにより、複雑な光線の経路を直進光におきかえることが可能になります。
(例題1)
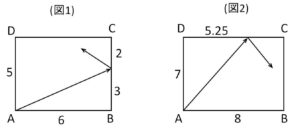
長方形内部の光の経路について考える。\(A\)から発射された光線は直進し、長方形の辺上にあたると等しい角度で反射する。またいずれかの頂点にあたると光は止まるとする。
(1)図1において、光は何回反射されてどの頂点で止まるか答えよ。
(2)図2において、光が止まるまでに動いた距離を求めよ。
(解答)
(1)
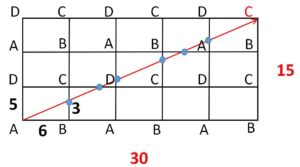
長方形を辺について次々と対称移動させると格子ができる。光の経路は直線で考えることができ、上図のようになる(縦について\(3k\)が\(5\)の倍数になるとき、\(3×5=15\) が最小。このとき横は\(6×5=30\))。格子線と交わる回数が反射の回数なので、その回数は\(6\)回。また頂点\(C\)で止まる。
(2)
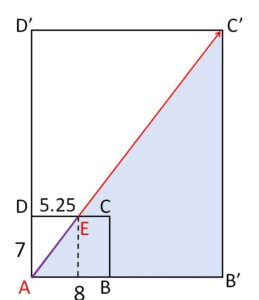
\(5.25k\) (\(k\)は自然数) が\(8\)の倍数となるような最小の\(k\)を求める。
\(5.25k=8l\) より
\(21k=32l\)
\(21\)と\(32\)は互いに素だから、最小の\(k\)は\(32\)、対応する\(l\)は\(21\)。(つまり縦方向に\(32\)個、横方向に\(21\)個長方形を並べればよい)
また図の\(AE\)は
\(AE=\sqrt{7^2+(\displaystyle\frac{21}{4})^2}\)
\(=7\sqrt{1+\displaystyle\frac{9}{16}}\)
\(=\displaystyle\frac{35}{4}\)
だから、光の動いた距離は
\(32AE=280\)
(例題2)
1辺の長さが\(2\)の正三角形\(ABC\)の中を直進する点がある。この点は、辺にあたると反射し、正三角形の頂点に達すると止まる。点は頂点\(A\)から動き始めるものとする。
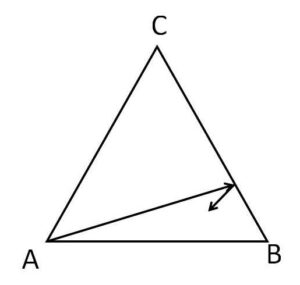
(1)辺\(BC\)を\(8\)等分し、\(B\)に最も近い点を\(P\)とする。点が最初\(P\)で反射するとき、何回反射してから止まるか。また点が動いた距離を求めよ。
(2)\(n\)を\(2\)以上の整数とする。辺\(BC\)を\(n\)等分し、\(B\)に最も近い点を\(Q\)とする。最初に\(Q\)で反射するとき、止まるまで何回反射するか\(n\)の式で表せ。
(解答)
(1)
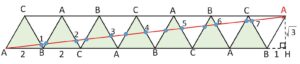
辺\(BC\)は\(7\)つの点で\(8\)等分される。
正三角形を折り返すことで点の経路を直線におきかえることができ、最初の三角形の\(BC\)と平行な辺と点の経路である直線との交点の個数は全部で\(7\)個なので、図のように上向きの三角形が\(7\)つ並ぶことになる。反射の回数は三角形の辺と直線の交点の個数で、最初の上向きの三角形だけ\(1\)点で交わるのでその個数は((2)も考慮すると)、
\(2×7-1=13\) (個)
より、\(13\)回反射する。また動いた距離は
高さ \(\sqrt{3}\)、底辺 \(2×7+1=15\)
の直角三角形より
\(\sqrt{15^2+3}=2\sqrt{57}\)
(2)
(1)と同様に考えると、上向きの三角形が\(n-1\)個並ぶことになる。点の経路(直線)と三角形の辺の交点の個数は、最初の三角形だけ\(1\)点で交わることに注意すると
\(2(n-1)-1=2n-3\) (個)
よって反射の回数は \(2n-3\) 回。
(もちろん \(n=8\) とすれば(1)の結果と一致する)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→外心 back→折り返しと平面図形