三角形の辺の大小と、対応する角の大小関係について見ていきます。
・三角形の辺の大小と角の大小
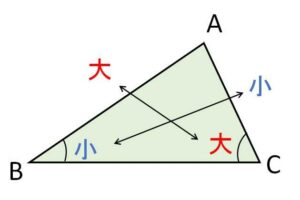
三角形の辺の大小と、辺に対応する角の大小は一致します。つまり次のことが成り立ちます。
\(△ABC\)において
(1)\(AB>AC\) \(⇔\) \(\angle C>\angle B\)
((1)’\(AB<AC\) \(⇔\) \(\angle C<\angle B\))
(2)\(AB=AC\) \(⇔\) \(\angle C=\angle B\)
(証明)
(1)’は(1)と同様、(2)は二等辺三角形の性質より分かるので、(1)を証明します。
(i)まずは\(→\)から
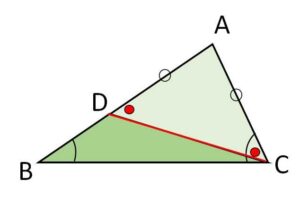
\(AD=AC\) となるように、\(AB\)上に\(D\)をとる。
二等辺三角形\(ADC\)の底角が等しいことと、\(△DBC\)の\(\angle D\)の外角に着目して
\(\angle C>\angle ACD\)・・・①
\(\angle ACD=\angle ADC\)・・・②
\(\angle ADC=\angle B+\angle DCB\) より
\(\angle ADC>\angle B\)・・・③
①②③をまとめると
\(\angle C>\angle B\)
(ii)次に\(←\)については背理法を用いる
条件より \(\angle C>\angle B\)・・・④
\(AB\)と\(BC\)の大小関係は
(ア)\(AB>AC\) (イ)\(AB<AC\) (ウ)\(AB=BC\)
のいずれか。
(イ)を仮定すると、(1)’の\(→\) より \(\angle C<\angle B\) となり④に矛盾。
(ウ)を仮定すると、(2)の\(→\) より \(\angle C=\angle B\) となり④に矛盾。
したがって(ア)となり
\(AB>AC\)
(この方法は転換法とよばれます。(1)(1)'(2)の条件(ア)(イ)(ウ)はすべての場合を網羅していて、結論も両立していないので使える方法です。このとき逆も真となります)
また最大辺に対応する角が最大角になるので、直角三角形・鈍角三角形の直角と鈍角に対応する辺は必ず最大辺になります。
(例題)
\(AB=AC\) である二等辺三角形\(ABC\)の辺\(BC\)上に\(B,C\)と異なる点\(P\)、\(BC\)の延長上に点\(Q\)をとる。このとき \(AP<AB<AQ\) であることを示せ。
角の大小は上記の定理の証明で使った 「2内角の和=外角」 を利用します。
(解答)
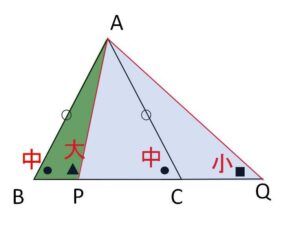
\(△ABC\)は二等辺三角形なので
\(\angle B=\angle C\)・・・①
また
\(\angle C+\angle PAC=\angle APB\) だから
\(\angle C<\angle APB\)・・・②
①②より
\(\angle B<\angle APB\) だから、\(△ABP\)に着目すると
\(AP<AB\)・・・③
次に
\(\angle Q+\angle CAQ=\angle C\) だから
\(\angle Q<\angle C\)・・・④
①④より
\(\angle Q<\angle B\) だから、\(△ABQ\)に着目すると
\(AB<AQ\)・・・⑤
したがって③⑤より
\(AP<AB<AQ\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の3辺の大小 back→角の二等分線の定理の逆