三角形の3辺の大小

(2辺の和)>残りの1辺　の定理について見ていきます。

 

・三角形の辺の大小
三角形の辺の長さについて次のことが成り立ちます。

(解説)

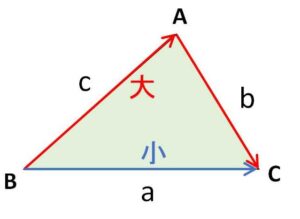
辺\(BC\)に着目すると、\(B \to C\) より \(B \to A \to C\) と移動したほうが遠回りになるので
\(b+c>a\)
となるということです。他の2辺についても同様なので
\(c+a>b\)、\(a+b>c\)
が成り立ち、不等式を変形すると差の形になるので(2)も成り立ちます。

これらの不等式をまとめると
\(|b-c|<a<b+c\)
となり、これは三角不等式とよばれます。または三角形の成立条件(必要十分条件)ともよばれ、逆にこの不等式が成り立つとき3辺を\(a,b,c\)とする三角形が存在することになります。(三角形が作られるためにはある程度の\(a,b,c\)の制限が必要になる)

 

(証明)

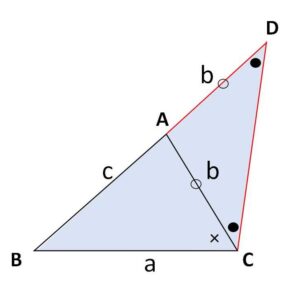
(角の二等分線の定理のときと同じ補助線をひく)
\(BA\)の延長上に、\(AD=AC\) となるような点\(D\)をとる。
すると、\(△ACD\)は二等辺三角形だから
\(\angle ACD=\angle ADC\)・・・①
また
\(\angle BCD>\angle ACD\)・・・②
だから①②より
\(\angle BCD>\angle ADC\)
よって\(△DBC\)に着目すると
\(b+c>a\)・・・③

同様に
\(c+a>b\)・・・④
\(a+b>c\)・・・⑤
が導ける。

次に③④⑤をまとめることを考える。
④⑤より
\(a>b-c\)、\(a>-(b-c)\)
だから \(a>|b-c|\)・・・⑥
③⑥より
\(|b-c|<a<b+c\)

※③④⑤より
\(a>b-c\)、\(a>-(b-c)\) の他に
\(b>c-a\)、\(b>-(c-a)\)
\(c>b-a\)、\(c>-(b-a)\)
も導けるので (2)(2辺の長さの差)<残りの1辺の長さ も成り立ちます。

 

(三角形の成立条件について)
\(△ABC\)の3辺が\(a,b,c\)のとき
「\(|b-c|<a<b+c\)」・・・(※)
が成り立ちますが、逆に(※)が成り立つとき\(a,b,c\)の3辺とする三角形が存在するかどうか検討してみます。

まず\(a,b,c\)が正になるかどうかを確認すると
\(|b-c|≧0\) だから、(※)より \(a>0\)

(i)\(b-c≧0\) のとき(※)より
\(b-c<b+c\) だから \(c>0\)。
\(b-c≧0\) より \(b≧c\) だから \(b>0\)。

(ii)\(b-c<0\) のとき(※)より
\(-(b-c)<b+c\) だから \(b>0\)。
\(b-c<0\) より \(b<c\) だから \(c>0\)。

次に三角形が存在するかどうか(作ることができるかどうか)を調べます。

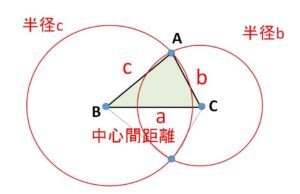
「\(|b-c|<a<b+c\)」・・・(※)
より、点\(B\)を中心とする半径\(c\)の円と点\(C\)を中心とする半径\(b\)の円は2点で交わる(外部・内部・外接内接の位置関係にない)ので、三角形を作ることができます。

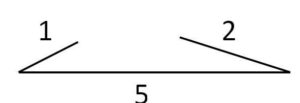
(※)を満たさない例えば
\(a=5\)、\(b=2\)、\(c=1\)
のケースだと辺が届かないので三角形が作られません(存在しない)。

 

演習は次回にします。

以上なります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の3辺の大小(例題)　back→三角形の辺と角の大小関係