三角形の3辺の大小関係や三角形の成立条件に関する例題です。
(例題1)
四角形\(ABCD\)において、\(AB,CD\)の中点をそれぞれ\(P,Q\)とするとき
\(PQ≦\displaystyle\frac{1}{2}(AD+BC)\)
であることを証明せよ。また等号が成立するとき、四角形\(ABCD\)がどのような四角形か答えよ。
(解答)
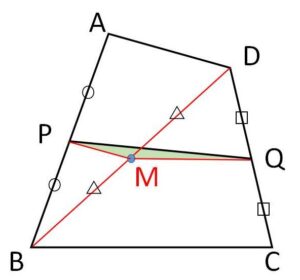
対角線\(BD\)の中点を\(M\)とする。
中点連結定理より
\(PM=\displaystyle\frac{1}{2}AD\)、\(MQ=\displaystyle\frac{1}{2}BC\)・・・①
また\(M\)が\(PQ\)上にないとき
\(PM+MQ>PQ\)
\(M\)が\(PQ\)上にあるとき
\(PM+MQ=PQ\)
だから合わせて
\(PM+MQ≧PQ\)・・・②
①を②に代入して
\(\displaystyle\frac{1}{2}(AD+BC)≧PQ\)
等号が成立するとき、\(P,M,Q\)は一直線上にあり、中点連結定理より
\(AD//PQ//BC\)
となるので、四角形\(ABCD\)は\(AD//BC\)の台形。
(例題2)
\(△ABC\)の辺\(BC\)の中点を\(M\)とするとき
\(AB+AC>2AM\)
を証明せよ。
(解答)
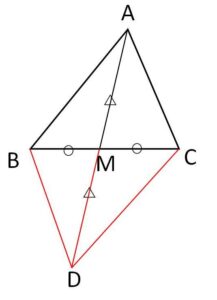
\(2AM=AD\) となるような\(D\)を\(AM\)の延長上にとる。
すると、四角形\(ABDC\)の対角線は互いに他を2等分しているので、四角形は平行四辺形になる。
よって、\(CD=AB\) となるから
\(AC+CD>AD\) より
\(AC+AB>2AM\)
(例題3)
3辺の長さが \(x+6,\ 3x-4,\ 2x^2-3x-5\) である三角形がある。実数\(x\)のとりうる範囲を求めよ。
(解答)
\((x+6)+(3x-4)>2x^2-3x-5\)・・・①
\((3x-4)+(2x^2-3x-5)>x+6\)・・・②
\((2x^2-3x-5)+(x+6)>3x-4\)・・・③
を満たせばよい。
①②③を整理して
\(2x^2-7x-7<0\)・・・①’
\(2x^2-x-15>0\)・・・②’
\(2x^2-5x+5>0\)・・・③’
\(2x^2-7x-7<0\)・・・①’
\((2x+5)(x-3)>0\)・・・②’
\(2x^2-5x+5>0\)・・・③’
③’の判別式は負の値なので、任意の\(x\)について③’は成り立つ。
よって①’②’を検討して
\(\displaystyle\frac{7-\sqrt{105}}{4}<x<\displaystyle\frac{7+\sqrt{105}}{4}\)
\(x<-\displaystyle\frac{5}{2},\ x>3\)
したがって共通部分を考えると、求める\(x\)の範囲は
\(3<x<\displaystyle\frac{7+\sqrt{105}}{4}\)
(\(10<\sqrt{105}<11\))
(注)
①②③を満たせば、各辺が正の値であることは保証されます(前回参照)。不安なら答えの範囲のときに正になるかどうか確かめてもよいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→中線定理 back→三角形の3辺の大小