垂心の性質について見ていきます。
・垂心
三角形の各頂点から、対辺またはその延長に下ろした3つの垂線は1点で交わり、この交点は垂心と呼ばれます。

(解説)
対辺またはその延長と指定しているのは、鋭角三角形・直角三角形・鈍角三角形で事情が異なるからです(垂心の位置も変わる) 。直角三角形では2つの垂線が三角形の2辺になっていて、直角をつくる頂点そのものが垂心になります。
また垂心では直角が複数出現するので、各点を通る円を用いると垂心に関する証明ができたり垂心の性質を導くことができます。
(証明)
(鋭角三角形について)
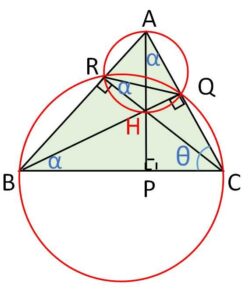
\(B,C\)から下ろした垂線の足を\(Q,R\)とし、これら2垂線の交点を\(H\)とする。\(A,H\)を直線で結び\(BC\)との交点を\(P\)とする。また補助線\(RQ\)をひく。
内接四角形の定理(対角の和が\(180°\))と、円周角の定理により各点を通る円が図のようにかける。すると円周角の定理より図の角\(α\)は全て等しい。
\(△BQC\)に着目すると
\(α+θ=90°\)
よって\(△APC\)に着目すると
\(\angle APC=90°\)
したがって\(AP\)も垂線になり、3垂線は\(H\)で交わる。
(直角三角形・鈍角三角形について)
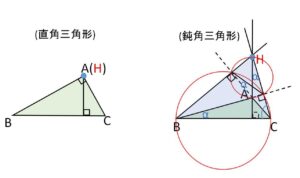
直角三角形では\(B,C\)から下ろした垂線は辺\(BA,CA\)になるので、2垂線の交点は\(A\)。また\(A\)から下ろした垂線は当然\(A\)を通るので、3垂線は\(A\)で交わりこれが垂心となる。
鈍角三角形では右図を使えば鋭角三角形と同様に証明できる。
・垂心の性質
直角三角形は特殊なので除くことにして、鈍角三角形は鋭角三角形と似たような内容になるので鋭角三角形についてのみ検討することにします。
①等しい角度(相似な直角三角形)の登場
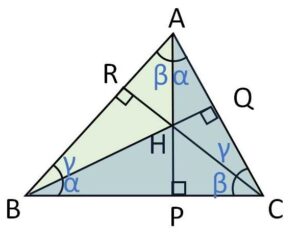
直角が多く登場するので、等しい角度が多数生まれます。
\(△APC\) と \(△BQC\) は \(\angle C\ (=β+γ)\) が共通の直角三角形なので相似であり、角\(α\)が等しくなります(証明の場合のように円を考えてもよい)。
同様に、図の\(β,γ\)同士も等しくなります。
②垂足三角形と角の二等分線
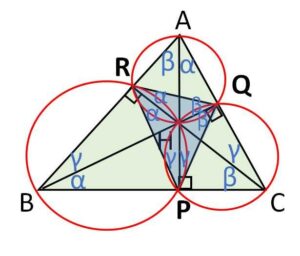
各頂点から対辺へ下ろした垂線の足3つを結んでできる三角形を垂足三角形といいます。図の\(△PQR\)は垂足三角形です。
これも各点を通る円をかくことで(図の3円はいずれも\(H\)を通る)、円周角の定理により図の\(α,β,γ\)同士が等しいことが分かります。
よって\(△ABC\)の3垂線は\(△PQR\)では角の二等分線になっていて、\(△ABC\)の垂心\(H\)は\(△PQR\)では内心になっています。(鈍角三角形では傍心になります)
③1頂点と垂線の足2つでできる三角形の相似
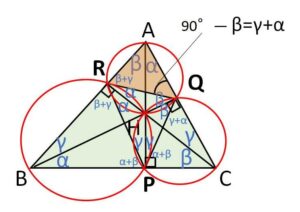
\(△AQR\)について、1つの角は\(\angle A\)。\(\angle AQR\)については
\(\angle AQR=90°-β=γ+α\) (\(α+β+γ=90°\) より)
よって\(△ABC\)と二角相等により、\(△AQR\)と\(△ABC\)は相似です。
同様に\(△PBR,△PQC\)も\(△ABC\)と相似です。
等しい角度が多く出現するので、他にも相似な三角形が存在します。
なお外心との関連もありますが、これは例題で扱うことにします。
(例題)
鋭角三角形\(△ABC\)の、辺\(BC,CA,AB\)の中点を\(L,M,N\)とする。\(BC,CA,AB\)の垂直二等分線の交点(外心)を\(O\)とすると、\(O\)は\(△LMN\)の垂心となることを示せ。
(解答)
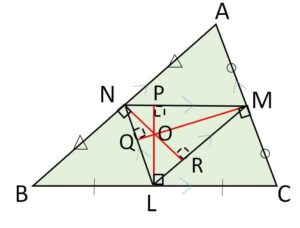
3つの垂直二等分線と\(△LMN\)の辺との交点を図のように\(P,Q,R\)とする。
中点連結定理より
\(NM//BC\)
であり、これと\(LP \perp BC\) より
\(LP \perp NM\)
同様に、\(MQ \perp LN\)、\(NR \perp ML\) となるので
3つの垂直二等分線は\(△LMN\)では頂点から対辺に下ろした垂線になる。
よって\(O\)は\(△LMN\)の垂心である。