傍心について見ていきます。
・傍心
三角形の1つ内角の二等分線と、他の2つの角の外角の二等分線は1点で交わり、この交点を傍心(ぼうしん)とよびます。
(証明)
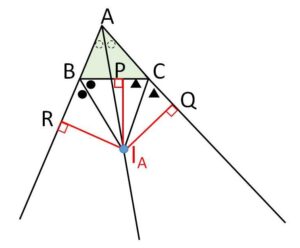
(証明は内心の場合とほとんど同じです。今回は角の二等分線が角を作る2直線から等距離にある点の集合であることを利用したいと思います)
\(B,C\)の箇所を外角に選ぶ。
\(B,C\)の外角の二等分線の交点を\(I_A\)とし、\(AI_A\)を結ぶ。\(I_A\)から\(BC\)と\(AC,AB\)の延長線へ垂線を下ろし、その足を\(P,Q,R\)とする。
\(I_A\)は\(B\)の外角の二等分線上にあるから
\(I_AR=I_AP\)・・・①
\(I_A\)は\(C\)の外角の二等分線上にもあるから
\(I_AP=I_AQ\)・・・②
①②より
\(I_AR=I_AQ\)
よって、\(I_A\)と\(AB,AC\)の延長線までの距離は同じだから、\(AI_A\)は内角\(A\)の二等分線となる。
したがって、内角\(A\)、外角\(B,C\)の二等分線は1点\(I_A\)で交わる。
また
\(I_AP=I_AQ=I_AR\)
と、これらの線分は三角形の辺またはその延長線と垂直であることから、\(I_A\)を中心とする\(P,Q,R\)を通る円は\(BC\)と\(AB,AC\)の延長線に接することになります。この円を傍接円とよびます。(一般的に内角の二等分線\(AI_A\)上には接点\(P\)はない)
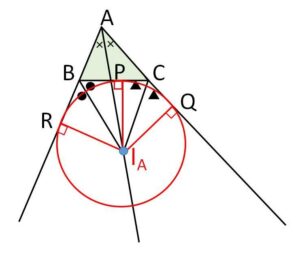
ところで、内角1つと外角2つの選び方は他に
\(B\)内角、\(A,C\)外角
\(C\)内角、\(A,B\)外角
もあるので、傍心と傍接円はそれぞれ全部で3個存在することになります。
(下図の■,●,▲同士は等しいので、傍心2つと頂点1つは1直線上にある。例えば\(I_C,A,I_B\))
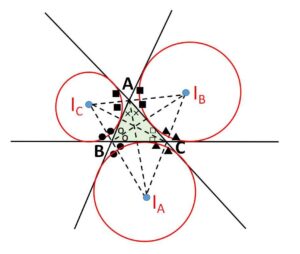
そこでこれらの傍心・傍接円を区別するために、例えば\(I_A\)では内角\(A\)の内部に位置していることから、角\(A\)内の傍心・傍接円とよぶこともあります。
・傍心の性質
傍心は角の二等分線の交点なので内心と同じような性質をもちます。
①面積
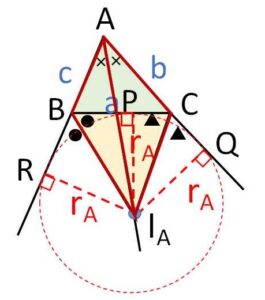
内心では三角形の和を考えましたが、傍心では差を考えます。
\(△ABC=△ACI_A+△ABI_A-△BCI_A\)
だから\(△ABC=S\)、角\(A\)内の傍接円の半径を\(r_A\)とおくと
\(S=\displaystyle\frac{1}{2}r_A(b+c-a)\)
3辺の長さ\(a,b,c\)が分かれば面積\(S\)も分かるので、\(r_A\)が求まる算段です。
同様に角\(B,C\)内の傍接円の半径\(r_B,r_C\)の関係式は次のようになります。
\(S=\displaystyle\frac{1}{2}r_B(c+a-b)\)
\(S=\displaystyle\frac{1}{2}r_C(a+b-c)\)
②傍心がつくる角
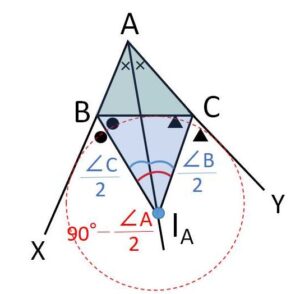
\(\angle AI_AB=\angle XBI_A-\displaystyle\frac{1}{2}\angle A\)
\(=\displaystyle\frac{1}{2}(\angle XBC-\angle A)\)
\(=\displaystyle\frac{1}{2}\angle C\)
同様に
\(\angle AI_AC=\displaystyle\frac{1}{2}\angle B\)
なので
\(\angle BI_AC=\displaystyle\frac{1}{2}(\angle C+\angle B)\)
\(=\displaystyle\frac{1}{2}(180°-\angle A)\)
\(=90°-\displaystyle\frac{1}{2}\angle A\)
残りの傍接円についても同様のことが成り立つ。
③外接円との関係
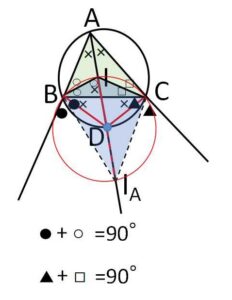
\(△ABC\)の内心を\(I\)として、\(AI\)(\(I_A\)も通る)と\(△ABC\)の外接円の交点を\(D\)とする。
\(\angle IBI_A=\angle ICI_A=90°\) だから
\(II_A\)を直径とする円は\(B,C\)を通る。
また\(△DBI,△DBC\)は二等辺三角形だから
\(DB=DI=DC\)
よって\(II_A\)を直径とする円の中心は\(D\)となるから
\(DI=DI_A\)
④傍心が作る三角形の垂心
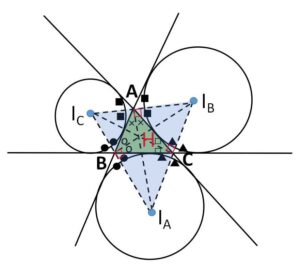
\(I_C,A,I_B\)は同一直線上にあるから
2■+2×=180°
よって
■+×=90°
となるから、\(I_AA\)は\(I_CI_B\)に下ろした垂線である。同様に\(I_BB,I_CC\)も垂線になるので、これら3垂線は1点\(H\)で交わり、\(H\)は\(△I_AI_BI_C\)の垂心となる。
またこれらの垂線は\(△ABC\)にとっては内角の二等分線になるので、\(H\)は\(△ABC\)の内心となります。
(例題)
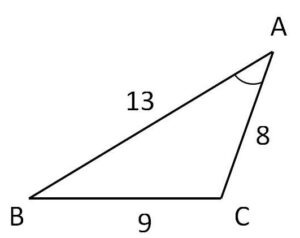
\(BC=9,\ CA=8,\ AB=13\) である\(△ABC\)がある。
(1)\(△ABC\)の面積を求めよ。
(2)\(BC\)、\(AB\)の延長線、\(AC\)の延長線に接する円の半径を求めよ。
(解答)
(1)
(余弦定理→正弦へ変換で解きます。ヘロンの公式でもよいです)
\(\cos A=\displaystyle\frac{13^2+8^2-9^2}{2\cdot13\cdot8}=\displaystyle\frac{19}{26}\)
よって
\(\sin A=\sqrt{1-(\displaystyle\frac{19}{26})^2}=\displaystyle\frac{3\sqrt{35}}{26}\)
だから
\(△ABC=\displaystyle\frac{1}{2}\cdot8\cdot13\cdot\displaystyle\frac{3\sqrt{35}}{26}\)
\(=6\sqrt{35}\)
(2)
(面積の差を考えます)
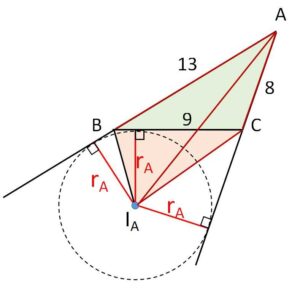
求める半径を\(r_A\)とする。
\(△ABC=△ABI_A+△ACI_A-△BCI_A\) より
\(6\sqrt{35}=\displaystyle\frac{1}{2}r_A(13+8-9)\)
よって
\(r_A=\sqrt{35}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→オイラー線 back→内心