チェバ・メネラウスの定理の逆(演習)

チェバの定理の逆と、メネラウスの定理の逆を利用した証明問題です。

(例題1)
\(△ABC\)内の任意の点\(O\)について、\(\angle BOC,\ \angle COA,\ \angle AOB\) の二等分線が辺\(BC,CA,AB\)と交わる点をそれぞれ\(P,Q,R\)とすれば、\(AP,BQ,CR\)は1点で交わることを証明せよ。

(解答)

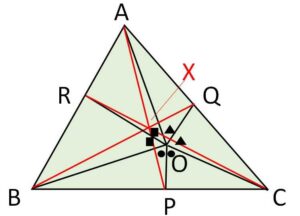
角の二等分線の定理より
\(\displaystyle\frac{BP}{PC}=\displaystyle\frac{OB}{OC}\)・・・①

\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{OC}{OA}\)・・・②

\(\displaystyle\frac{AR}{RB}=\displaystyle\frac{OA}{OB}\)・・・③

①②③の辺々を掛けると
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=\displaystyle\frac{OB}{OC}\cdot\displaystyle\frac{OC}{OA}\cdot\displaystyle\frac{OA}{OB}\)

よって
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
だからチェバの定理の逆より、\(AP,BQ,CR\)は1点で交わる。

(注)
チェバの定理の逆は2つの仮定が必要でした。1つ目は\(P,Q,R\)の位置についてですが、今回は3点とも辺上にあるのでOK。2つ目は\(BQ,CR\)が交わる(平行でない)ことですがこれもOK。(2つ目は3点が辺上にある場合には必ず交わるので今回は気にしなくても大丈夫です)

(例題2)
平行四辺形\(ABCD\)の辺\(AB,BC\)上の点をそれぞれ\(E,F\)とし、\(AF,CE\)の交点を\(P\)とする。\(E\)を通る\(AD\)に平行な直線と、\(F\)を通る\(AB\)に平行な直線の交点を\(Q\)とする。このとき3点\(P,Q,D\)は一直線上にあることを示せ。

(解答)

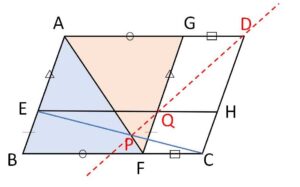
図のように\(G,H\)を設定する。
\(△ABF\)と直線\(EC\)についてメネラウスの定理より
\(\displaystyle\frac{AE}{EB}\cdot\displaystyle\frac{BC}{CF}\cdot\displaystyle\frac{FP}{PA}=1\)・・・①
また
\(\displaystyle\frac{AE}{EB}=\displaystyle\frac{GQ}{QF}\)、\(\displaystyle\frac{BC}{CF}=\displaystyle\frac{AD}{DG}\)
これらを①に代入して
\(\displaystyle\frac{GQ}{QF}\cdot\displaystyle\frac{AD}{DG}\cdot\displaystyle\frac{FP}{PA}=1\)
並び変えると
\(\displaystyle\frac{AD}{DG}\cdot\displaystyle\frac{GQ}{QF}\cdot\displaystyle\frac{FP}{PA}=1\)
となるから、メネラウスの定理の逆より3点\(P,Q,D\)は一直線上にある。

(注)
メネラウスの定理の逆の条件「3点のうち、1点が辺の延長上(2点は辺上)」を満たします。本問では\(△AGF\)において辺の延長にある1点は\(D\)、辺上にある2点は\(P,Q\)です。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円周角の定理　back→チェバ・メネラウスの定理の逆