円周角の定理

円に関する性質や定理について整理していきます。
今回は円周角の定理がメインテーマです。

・円
平面上で、点\(O\)からの距離が一定値\(r \ (>0)\)である点の集合を円といい、点\(O\)を円の中心、\(r\)を円の半径といいます。

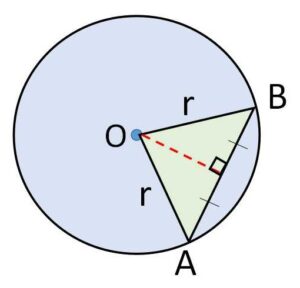
この定義により、円周上の異なる2点\(A,B\)と中心\(O\)で作られる三角形は二等辺三角形になり、\(O\)から\(AB\)に中線を下ろすと垂線になります。

・円周角の定理

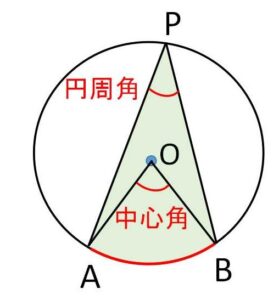
円弧(円周の一部)\(AB\)が与えられたとき、弧\(AB\)以外の円周上の点を\(P\)とすると、\(\angle APB\)を弧\(AB\)に対する円周角とよびます。(単に弧\(AB\)というと大きい方の弧の場合も考えられるので、図の小さい方の弧\(AB\)を劣弧とよぶこともあります。大きい方は優弧です)
また円弧\(AB\)が作る扇形の\(\angle AOB\)を弧\(AB\)に対する中心角とよびます。
円周角には次の重要な性質があります。

(円周角の定理)
1つの弧に対する円周角の大きさは一定である。また円周角の大きさはこの弧に対する中心角の大きさの半分である。
特に半円の弧に対する円周角は\(90°\)である。

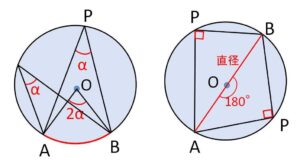
また円周角の定理により次の事も成り立ちます。

(証明)

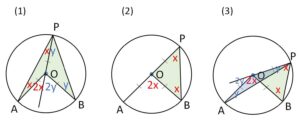
(中心\(O\)の位置により図形の位置関係が変わるので場合分けします。いずれも内角の和が外角にあることを利用します)

(1)\(\angle APB\)の内部に\(O\)がある
\(\angle APO=x\)、\(\angle BPO=y\) とおくと
\(\angle AOB=2x+2y\)
よって
\(\angle AOB=2\angle APB\)

(2)\(AP\) or \(BP\) 上に\(O\)がある
\(\angle AOB=2\angle APB\)

(3)\(\angle APB\)の外部に\(O\)がある
\(\angle BPO=x\)、\(\angle APO=y\)とおくと
\(\angle AOB=2x-2y\)
よって
\(\angle AOB=2\angle APB\)

したがって、いずれの場合も中心角\(\angle AOB\) は固定されているのでその角を\(2α\)とおけば、\(P\)がどの位置にある場合も円周角は\(α\)となり一定である。特に弧が半円になる場合には\(2α=180°\) だから \(α=90°\) となる。

また円周角が\(α°\)である弧の長さ\(l\)は、中心角が\(2α°\)であることから半径を\(r\)とおけば
\(l=2πr\cdot\displaystyle\frac{2α}{360}\)
となり、\(r\)は定数なので円弧の長さと円周角は比例することになる。

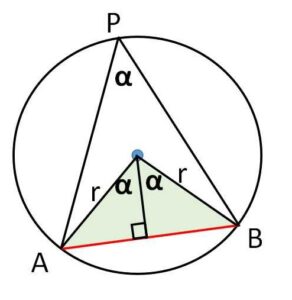
なお弦の長さと円周角の大きさは比例しない。その理由は弦の長さが\(α\)の三角比で表されるからで、図より
\(AB=2r\sinα\)
ただし\(α\)が等しければ\(\sinα\)も等しいので、同じ大きさの円周角をもつ2つの円弧に関する弦の長さは等しくなる。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円周角の定理の逆・円の内部外部と円周角　back→チェバ・メネラウスの定理の逆(演習)