円周角の定理の逆・円の外部内部と円周角

円周角の定理とそれを拡張させた事項について見ていきます。

・円周角の定理の逆
ある弧(円周の一部)に対する円周角は一定であるというのが円周角の定理でしたが、その逆についても成り立ちます。

(円周角の定理の逆)
4点\(A,B,P,Q\)があり、直線\(AB\)に関して\(P,Q\)は同じ側にあるとする。このとき \(\angle APB=\angle AQB\) ならば、4点\(A,B,P,Q\)は同一円周上にある。

(解説)

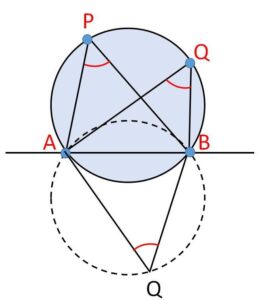
円周角逆1

同一直線上にない異なる3点を通る円は存在しますが、4点を通る円は必ずしも存在しません。しかし4点を通る円が存在するというのがこの定理です。\(AB\)に関して同じ側という条件があるのは、\(\angle APB=\angle AQB\) となる\(P,Q\)が\(AB\)に関して反対側にとることができ、同一円周上に位置しないことがあるからです。

(証明)
(背理法と三角形の内角と外角の関係を利用します)
\(A,P,B\)を通る円を考える。\(Q\)がこの円周上にないと仮定すると、\(Q\)は円の内部か外部にある。

(i)\(Q\)が円の内部にあるとき

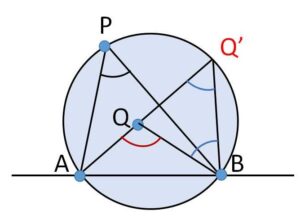
円周角逆2

\(AQ\)と円の交点を\(Q’\)とする。三角形の内角と外角の関係より
\(\angle AQB=\angle QQ’B+\angle QBQ’\)
だから
\(\angle AQB>\angle QQ’B\)・・・①
また円周角の定理より
\(\angle APB=\angle QQ’B\)・・・②
①②より
\(\angle AQB>\angle APB\) となるから
\(\angle AQB=\angle APB\) に矛盾。

(ii)\(Q\)が円の外部にあるとき

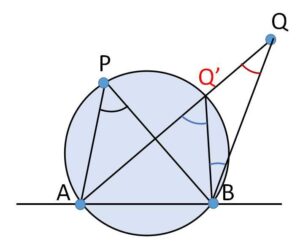
円周角逆3

\(AQ\)と円の交点を\(Q’\)とする。三角形の内角と外角の関係より
\(\angle AQB=\angle AQ’B-\angle Q’BQ\)
だから
\(\angle AQB<\angle AQ’B\)・・・③
また円周角の定理より
\(\angle APB=\angle AQ’B\)・・・④
③④より
\(\angle AQB<\angle APB\) となるから
\(\angle AQB=\angle APB\) に矛盾。

以上より\(Q\)は円周上にあることが分かる。

・円の内部外部と円周角
円周角の定理の逆の証明の内容を考えると、円の内部外部の点が作る角と円周角の大小関係について次のことが成り立つことが分かります。(中学の復習でないかもしれませんがここで扱っておきます)

(円との位置関係と角の大小)
4点\(A,B,P,Q\)があり、直線\(AB\)に関して\(P,Q\)は同じ側にあるとする。\(A,P,B\)を通る円について
(1)\(Q\)が円の内部 \(⇔\) \(\angle APB<\angle AQB\)
(2)\(Q\)が円の外部 \(⇔\) \(\angle APB>\angle AQB\)
(3)\(Q\)が円周上 \(⇔\) \(\angle APB=\angle AQB\)

(解説)

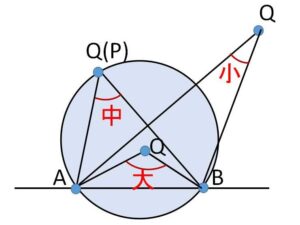
円周角逆4

(3)は円周角の定理とその逆です。(1)(2)についても同様に証明可能ですが、これらは図を書くと判断可能なので覚えやすいと思います。

(証明)
(1)(2)の\(→\)は円周角の定理の逆の証明内容を参考にすれば示せます。逆も背理法を利用すればOKです。(3)は円周角の定理とその逆なので省略します。

(1)\(→\)について

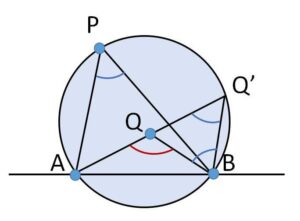
円周角逆5

\(Q\)は円の内部にあり
\(\angle AQB=\angle AQ’B+\angle QBQ’\)
よって
\(\angle AQB>\angle AQ’B\)
また円周角の定理より
\(\angle APB=\angle AQ’B\) だから
\(\angle AQB>\angle APB\)

(2)\(→\)について

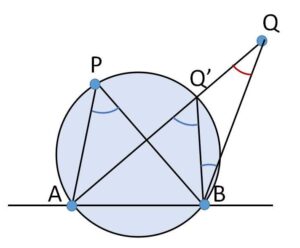
円周角逆6

\(Q\)は外部にあり
\(\angle AQB=\angle AQ’B-\angle Q’BQ\)
よって
\(\angle AQB<\angle AQ’B\)
また円周角の定理より
\(\angle APB=\angle AQ’B\)
ゆえに
\(\angle AQB<\angle APB\)

以上のことをまとめると円周角の定理も含めて
(1)\(Q\)が円の内部 \(→\) \(\angle APB<\angle AQB\)
(2)\(Q\)が円の外部 \(→\) \(\angle APB>\angle AQB\)
(3)\(Q\)が円周上 \(→\) \(\angle APB=\angle AQB\)
ですが、これを利用して背理法で逆が証明できます。

(逆)
(1)\(←\)について (内部であることの証明)
\(Q\)が内部にないと仮定すると、\(Q\)は円の外部か円周上にある。すると(2)(3)の\(→\)より
\(\angle APB≧\angle AQB\)
となるが、仮定 \(\angle APB<\angle AQB\) に矛盾。
よって、(1)の逆は成り立つ。

(2)\(←\)について (外部であることの証明)
\(Q\)が外部にないと仮定すると、\(Q\)は円の内部か円周上にある。すると(1)(3)の\(→\)より
\(\angle APB≦\angle AQB\)
となるが、仮定 \(\angle APB>\angle AQB\) に矛盾。
よって、(2)の逆は成り立つ。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の接線　 back→円周角の定理