内接円の接線の長さについて見ていきます。
・接線の長さ
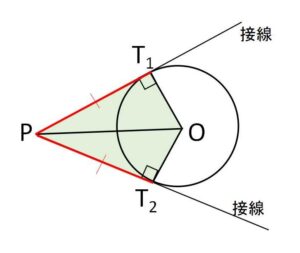
円の外部にある点\(P\)から円に2本の接線をひくと、\(P\)からそれぞれの接点\(T_1,T_2\)までの長さ(接線の長さという)は等しくなります。つまり
\(PT_1=PT_2\)
これは2つの直角三角形の合同(斜辺共通、1辺は半径と同じで等しい)から分かります。
・三角形の内接円と接線の長さ
上記の通り接線の長さが等しいことから、三角形に内接する円と辺の長さについて次のことが分かります。
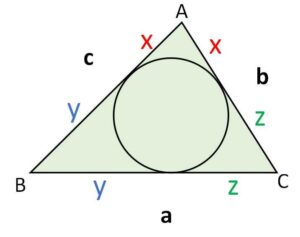
図のように三角形の辺の長さを\(a,b,c\)とし、各頂点と接点までの長さを\(x,y,z\)とおくと
\(y+z=a\)・・・①
\(z+x=b\)・・・②
\(x+y=c\)・・・③
が成り立ち、\(x,y,z\)を求めると (①+②+③)÷2 より
\(x+y+z=\displaystyle\frac{1}{2}(a+b+c)\)
なので、これから①②③をそれぞれ引くことにより
\(x=\displaystyle\frac{1}{2}(-a+b+c)\)
\(y=\displaystyle\frac{1}{2}(a-b+c)\)
\(z=\displaystyle\frac{1}{2}(a+b-c)\)
となります。よって3辺の長さが分かっていると各頂点からの接線の長さが求まることになります。
・四角形の内接円と接線の長さ
四角形に内接する円が存在する場合(四角形が円に外接する場合)、接線の長さが等しいことにより辺の長さについて次のことが成り立ちます。
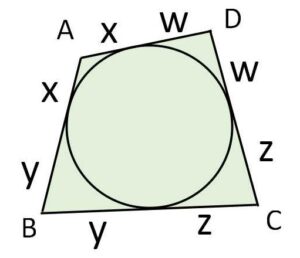
対辺の和を考えると
\(AB+CD=BC+DA\)・・・④
\(=(x+y+z+w)\)
(参考)
三角形と違って、四角形の場合は内接円が必ずしも存在しません。実は対辺の和が等しいという④式は必要十分条件であり、逆に④が成り立つ場合には四角形に内接する円が存在することになります(証明略)。よって④が成り立つかどうかが内接円が存在する判別方法になります。
・台形と内接円
円に外接する四角形が台形である場合の特殊例について検討してみます。もちろん上記のように対辺の和が等しいこと④も成り立ちますが、台形の平行線に着目すると相似形が見えてきます。
内接円の中心\(O\)は四角形(台形)の内角の二等分線上にあり、\(O\)から各辺に垂線をおろすと垂線の足は円との接点です。
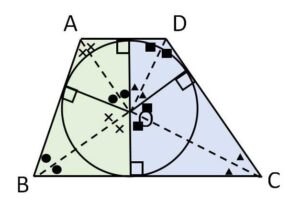
左上の\(AO\)を斜辺とする直角三角形の鋭角を●×とすると
●+×=90°
\(AD//BC\)より \(\angle A+\angle B=180°\) だから、左下の\(BO\)を斜辺とする直角三角形の鋭角も●×。よってこれらの三角形は相似になります。右側についても同様です。
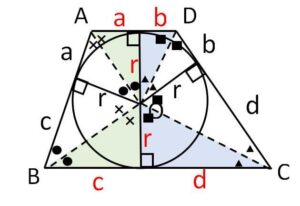
すると円の半径を\(r\)、各接線の長さを図のように\(a,b,c,d\)とおくと、
左側の三角形の相似により
\(\displaystyle\frac{a}{r}=\displaystyle\frac{r}{c}\)
よって
\(ac=r^2\)
同様に \(bd=r^2\) だから
\(ac=bd=r^2\)・・・⑤
したがって台形の4辺の長さ(3辺でも④より残りが分かる)が分かっていれば図より\(b,c,d\)はすべて\(a\)のみで表すことができ、⑤の \(ac=bd\) より\(a\)が決定できます。すると\(b,c,d\)も求まり、内接円の半径\(r\)も⑤より求まります。
(例題)
直角三角形\(ABC\)の内接円が斜辺\(BC\)に接する点を\(T\)とすれば、\(BT\cdot CT\)はこの直角三角形の面積に等しいことを示せ。
(解答)
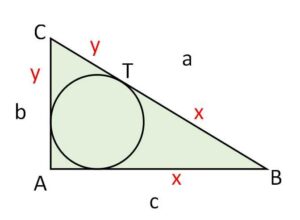
図のように3辺を\(a,b,c\)とおくと
\(x=BT=\displaystyle\frac{1}{2}(a-b+c)\)
\(y=CT=\displaystyle\frac{1}{2}(a+b-c)\)
よって
\(BT \cdot CT\)
\(=\displaystyle\frac{1}{4}\{a-(b-c)\}\{a+(b-c)\}\)
\(=\displaystyle\frac{1}{4}\{a^2-(b-c)^2\}\)
\(=\displaystyle\frac{1}{4}\{a^2-(b^2+c^2)+2bc\}\)
ここで三平方の定理より
\(a^2=b^2+c^2\)
だから
\(BT \cdot CT=\displaystyle\frac{1}{2}bc\)
これは直角三角形\(ABC\)の面積である。
(例題2)
図のように円に外接している台形がある。
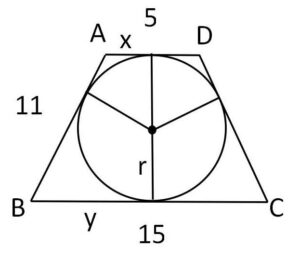
(1)\(CD\)の長さを求めよ。
(2)図の接線の長さ\(x,y\)を求めよ。
(3)円の半径を求めよ。
(解答)
(1)
\(5+15=11+CD\) より
\(CD=9\)
(2)
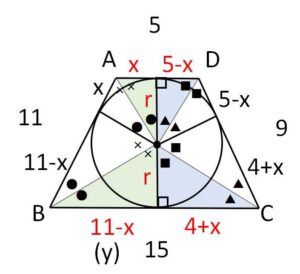
\(x\)を用いると、各接線の長さは図のように表される。
直角三角形の相似より
\(x(11-x)=(5-x)(4+x)\ (=r^2)\)
よって
\(11x=x+20\)
\(x=2\)
ゆえに
\(y=11-x=9\)
(3)
\(r^2=2\cdot9=18\) より
\(r=3\sqrt{2}\)
(別解)
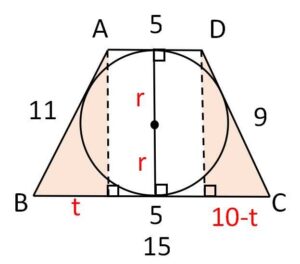
\(A,D\)から垂線を下ろして、図のように\(t\)を設定する。
2つの直角三角形は高さが\(2r\)で共通だから三平方の定理より
\(11^2-t^2=9^2-(10-t)^2\ (=(2r)^2)\)
整理して
\(121=81-100+20t\)
\(t=7\)
よって
\(4r^2=121-49=72\)
\(r^2=18\)
\(r=3\sqrt{2}\)
(このように\(r\)を先に求めて、(2)の\(x,y\)を相似を利用して求めてよいです)
以上になります。お疲れ様です。
ここまで見て頂きありがとうございました。
next→傍接円と接線の長さ back→内接四角形の定理