傍接円と接線の長さ

傍接円に関する接線の長さについて見ていきます。

 

・傍接円と接線の長さ
傍接円の接線の長さも、内接円の場合と同様に連立方程式を立てて解くことで求めることができます。
傍接円は全部で3個存在しますが、\(\angle A\) 内の傍接円(\(BC\)、\(AB\)の延長、\(CA\)の延長に接する円)について検討してみます。(残りの2つも同様に考えることができます)

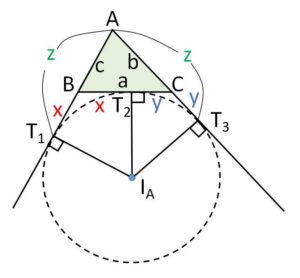
3辺が\(a,b,c\)の三角形において、各頂点からの接線の長さを図のように\(x,y,z\)とおくと

\(x+y=a\)・・・①
\(z-x=c\)・・・②
\(z-y=b\)・・・③

となるので①②③より\(x,y,z\)を求めると、(①+②+③)÷2 より\(z\)が求まり、これと②③から\(x,y\)が求まりその結果は

\(x=\displaystyle\frac{1}{2}(a+b-c)\)
\(y=\displaystyle\frac{1}{2}(a-b+c)\)
\(z=\displaystyle\frac{1}{2}(a+b+c)\)

となります。一番長い接線の長さ\(z\)は和の形になっていて、他の2つは差の形になっています。また\(\angle A\)内の傍接円では\(A\)に対応する辺の長さ\(a\)についてはすべて\(+a\)になってるところがポイントです。

 

 

(例題)
\(AB=7,BC=5,CA=6\) の三角形\(ABC\)がある。また\(BC\)、\(AB\)の延長、\(AC\)の延長と接している円があり、それぞれの接点を\(D,E,F\)とする。このとき、\(AE,BD,CF\)の長さをそれぞれ求めよ。

 

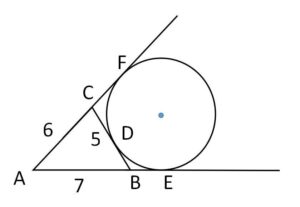
(解答)

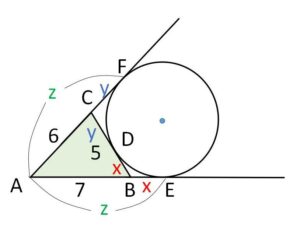
\(AE=z\)、\(BD=x\)、\(CF=y\) とおくと図より

\(x+y=5\)・・・①
\(z-x=7\)・・・②
\(z-y=6\)・・・③

①②③より
\(x=2\)、\(y=3\)、\(z=9\)
よって
\(AE=9\)、\(BD=2\)、\(CF=3\)

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接弦定理とその逆　back→内接円と接線の長さ