接弦定理とその逆

接弦定理について見てきます。

 

・接弦定理
円の接線と弦が作る角と円周角について次のことが成り立ちます。

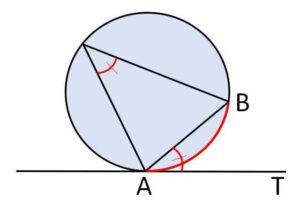
(解説)
弦と接線が作る角の定理です。単に弧\(AB\)に対する円周角とすると2つの円周角が存在しますが、このうち\(\angle BAT\)と等しいのはこの角内にある弧\(AB\)に対する円周角です。(もう1つの円周角は内接四角形の定理より\(180°-\angle BAT\))
証明は円周角の定理と、\(A\)を通る接線に垂直な直線は円の中心を通る(直径と重なる)ことを利用します。ただし\(\angle BAT\)が「鋭角・直角・鈍角」で様子が異なるので場合分けします。

(証明)
(i)\(\angle BAT\)が鋭角の場合

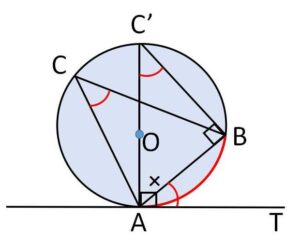
\(A\)を通る円の直径を\(AC’\)とすると、\(\angle ABC’=90°\) だから
\(\angle AC’B=90°-\angle BAC’\)・・・①
\(AC’\)は接線\(AT\)に垂直だから
\(\angle BAT=90°-\angle BAC’\)・・・②
①②より
\(\angle BAT=\angle AC’B\)・・・③
また円周角の定理より
\(\angle ACB=\angle AC’B\)・・・④
よって③④より
\(\angle BAT=\angle ACB\) (題意)

(ii)\(\angle BAT\)が直角の場合

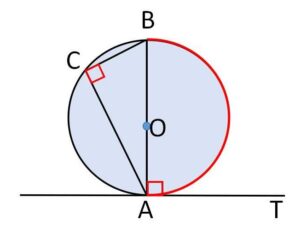
\(AB\)は円の直径になるので
\(\angle BAT=\angle ACB\ (=90°)\)

(iii)\(\angle BAT\)が鈍角の場合

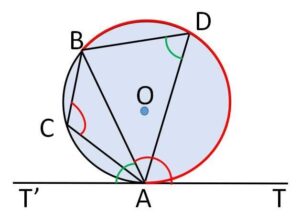
接線上に\(T\)の反対側に\(T’\)をとると
\(\angle BAT=180°-\angle BAT’\)・・・⑤
\(\angle BAT’\)は鋭角だから(i)より
\(\angle BAT’=\angle ADB\)・・・⑥
また内接四角形の定理より
\(\angle ACB=180°-\angle ADB\)・・・⑦
⑥⑦より
\(\angle ACB=180°-\angle BAT’\)・・・⑧
よって⑤⑧より
\(\angle BAT=\angle ACB\)

 

 

・接弦定理の逆
上記接弦定理の逆も成り立ちます。

(解説)
接線と弦のつくる角が円周角に等しいことが接弦定理で、逆に角が等しいとき接線になることが接弦定理の逆です。

(証明)

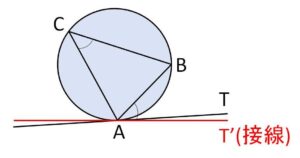
(同一法を利用します)
\(A\)を通る円\(O\)の接線\(AT’\)を\(T,T’\)が\(AB\)に関して同じ側にあるようにとる。
接弦定理により
\(\angle BAT’=\angle ACB\)
仮定より
\(\angle BAT=\angle ACB\)
従って
\(\angle BAT’=\angle BAT\)
となるので、\(AT,AT’\)は一致し、\(AT\)も接線となる。

 

 

(例題)
図のように円\(O\)と円\(O’\)が点\(B\)で接していて(共通接線をもち)、また\(AC\)は点\(T\)で円\(O’\)と接している。このとき\(BT\)は\(\angle ABC\)を二等分することを示せ。

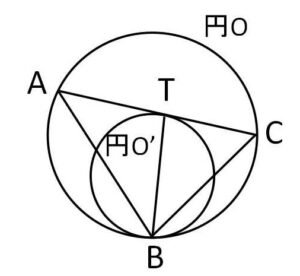
(解答)

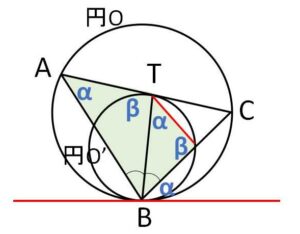
\(B\)を通る接線で円\(O,O’\)について接弦定理より、図の\(α\)同士は等しい。
また\(T\)を通る接線で円\(O’\)について接弦定理より、図の\(β\)同士は等しい。
よって
\(\angle ABT=\angle CBT\ (=180-(α+β))\)
となるから、\(BT\)は角の二等分線となる。

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→方べきの定理　back→傍接円と接線の長さ