方べきの定理の逆について見ていきます。
・方べきの定理の逆
点\(P\)を2つの線分\(AB,CD\)の交点、またはそれらの延長のただ1つの交点とする。このとき
\(PA\cdot PB=PC\cdot PD\) が成り立つならば、4点\(A,B,C,D\)は同一円周上にある。
(解説)
\(P\)の位置が
(1)\(AB,CD\)いずれも線分上
(2)\(AB,CD\)いずれも延長上
の場合があり、証明もこれらで場合分けします(内容の大部分は同じで、方べきの定理と同様に相似を利用します)。片方は線分上でもう一方は延長上にある場合は4点が同一円周上にあるという結論を導くことができずダメです。
(証明)
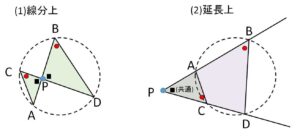
仮定 \(PA\cdot PB=PC\cdot PD\) より
\(PA:PD=PC:PB\)
また \(\angle APC=\angle DPB\) より、2辺の比とはさむ角が等しいから
\(△APC ∽ △DPB\)
よって \(\angle PCA=\angle PBD\)
したがって
(1)線分上にある場合は、直線\(PD\)に関して同じ側に\(C,B\)があるので円周角の定理の逆より4点は同一円周上にあることが分かる。
(2)延長上にある場合は、四角形が円に内接する条件(内接四角形の定理の逆)より4点は同一円周上にあることが分かる。
(注)片方の線分上、もう一方の延長上にある場合
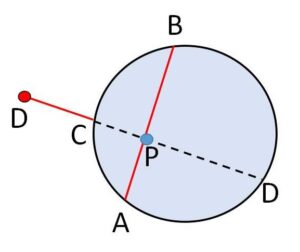
上図のように\(△ABC\)の外接円(3点を通る唯一の円)上に\(D\)が存在しないので、4点は同一円周上に存在しません。
また片方が接線の場合の方べきの定理の逆も成立します。
一直線上にない3点\(A,B,T\)と、\(AB\)の延長上に\(P\)がある。このとき
\(PA\cdot PB=PT^2\) が成り立つならば、\(PT\)は\(A,B,T\)を通る円に接する。
3点が同一直線上にあると、これら3点を通る円は存在しないので除外しています。また接線\(PT\)が存在するように\(P\)は\(AB\)の延長にとります(\(P\)が円の外部にあるようにする)。証明は同様に相似を利用します。
(証明)
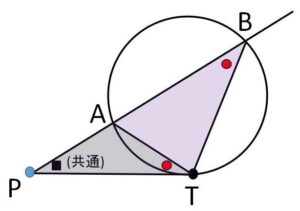
仮定 \(PA\cdot PB=PT\cdot PT\) より
\(PA:PT=PT:PB\)
また \(\angle APT=\angle TPB\) より、2辺の比とはさむ角が等しいので
\(△APT ∽△TPB\)
よって
\(\angle ATP=\angle TBP\)
したがって接弦定理の逆より、\(PT\)は\(A,B,T\)を通る円に接する。
(例題)
2円\(O,O’\)が2点\(P,Q\)で交わっている。\(PQ\)の延長上の点\(R\)から、円\(O,O’\)にそれぞれ\(A,B\)および\(C,D\)で交わる直線を引くと、4点\(A,B,C,D\)は同一円周上にあることを示せ。ただし\(A,B,C,D\)は一直線上にないものとする。
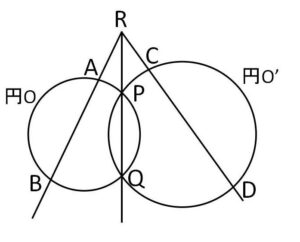
(解答)

円\(O\)と点\(R\)について方べきの定理より
\(RA\cdot RB=RP\cdot RQ\)・・・①
円\(O’\)と点\(R\)について方べきの定理より
\(RC\cdot RD=RP\cdot RQ\)・・・②
①②より
\(RA\cdot RB=RC\cdot RD\)
したがって\(AB,CD\)の延長の交点が\(R\)だから、方べきの定理の逆より\(A,B,C,D\)は同一円周上にある。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→トレミーの定理 back→方べきの定理