方べきの定理

方べきの定理について見ていきます。

・方べきの定理①(基本型)
円に関する線分の長さについて次のことが成り立ちます。

(方べきの定理①:基本型)
円\(O\)の周上にない点\(P\)を通る2直線が、円\(O\)とそれぞれ2点\(A,B\)、2点\(C,D\)で交わっている。このとき
\(PA\cdot PB=PC\cdot PD\)

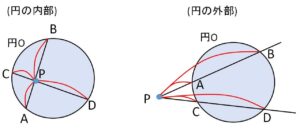
(解説)
点\(P\)の位置が円の内部か外部かで図は異なりますが、結果と証明の大部分は同じです。
証明は相似な2つの三角形の線分比を考えますが、円に特有な定理(円周角の定理・内接四角形の定理)を利用します。

(証明)

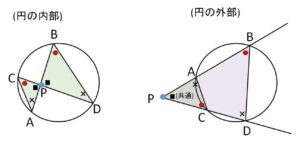
いずれの図においても
\(△PAC ∽ △PDB\)
よって
\(\displaystyle\frac{PA}{PC}=\displaystyle\frac{PD}{PB}\)
ゆえに
\(PA\cdot PB=PC\cdot PD\)

(参考)

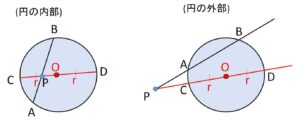
\(PA\cdot PB=PC\cdot PD\)
は\(P\)を通る任意の2直線(それぞれ円と2交点をもつ)について成り立つので、片方の直線を円の中心を通るようにすると

(内部)
\(PA \cdot PB=PC \cdot PD\)
\(=(r-PO)(r+PO)\)
\(=r^2-PO^2\)
(外部)
\(PA \cdot PB=PC \cdot PD\)
\(=(PO-r)(PO+r)\)
\(=PO^2-r^2\)

となり、直線\(APB\)は自由に選べるので、\(P\)が定点だといずれも直線の選び方によらず線分の積は一定値になる。この一定値 \(r^2-PO^2,PO^2-r^2\) は円\(O\)に対する点\(P\)の方べきの値とよばれる。詳細は不明だが「方べき」の「べき(冪)」は、同じ数や文字を繰り返し掛けたもので、\(PO^2,r^2\)がこれにあたり、「方」は四角形の意味で、\(PA \cdot PB,PC \cdot PD\)が四角形(長方形)の面積とみなせることに対応します。

・方べきの定理②(接線型)
点\(P\)が外部にあるとき、片方の直線が接線であっても同様の定理が成り立ちます。

(方べきの定理②:接線型)
円外の点\(P\)を通る2直線の一方が円と2点\(A,B\)で交わり、もう一方が点\(T\)で接しているとする。このとき
\(PA\cdot PB=PT^2\)

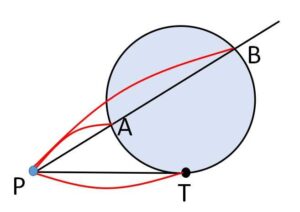
(解説)
方べきの定理①の2点\(C,D\)が1点\(T\)に重なるとして
\(PA \cdot PB=PT\cdot PT\)
とみれば定理②は定理①の特殊例とみることもできます。
証明は接弦定理を利用し、同様に相似な三角形の辺の比を考えます。

(証明)

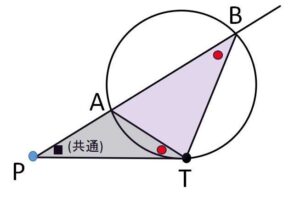
\(△APT∽△TPB\) より
\(\displaystyle\frac{PA}{PT}=\displaystyle\frac{PT}{PB}\)
よって
\(PA\cdot PB=PT^2\)

(例題)
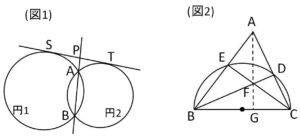
(1)図1において2円は2点\(A,B\)で交わっており、直線\(ST\)は2円に接する直線で\(S,T\)は接点である。直線\(ST,AB\)の交点を\(P\)とすると、\(PS=PT\)であることを示せ。

(2-1)図2において半円と三角形が交わっており、\(BC\)は直径である。このとき
\(BA\cdot BE=BC\cdot BG\) を示せ。
(2-2)\(BA\cdot BE+CA\cdot CD=BC^2\) を示せ。

(解答)
(1)
2円について方べきの定理より
\(PA\cdot PB=PS^2\)・・・①
\(PA\cdot PB=PT^2\)・・・②
①②より
\(PS^2=PT^2\)
\(PS=PT\)

(2-1)

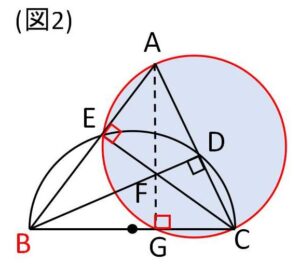
\(A,E,G,C\)は同一円周上にあるので、この円で方べきの定理より
\(BA\cdot BE=BC\cdot BG\)

(2-2)

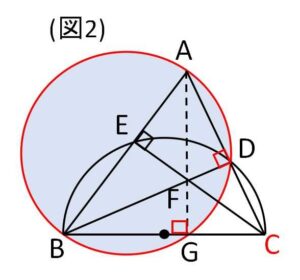
\(A,D,G,B\)は同一円周上にあるので、方べきの定理より
\(CA\cdot CD=CB \cdot CG\)

よって(2-1)も合わせると
\(BA\cdot BE+CA\cdot CD\)
\(=BC\cdot BG+CB\cdot CG\)
\(=BC(BG+GC)\)
\(=BC^2\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→方べきの定理の逆　back→接弦定理とその逆