共通接線の長さ

2円の共通接線に関する事項について整理します。

 

・共通外接線・内接線の長さ
2円の位置関係が (1)外部 または (2)外接 する場合について検討します。
共通接線と2円の接点を\(A,B\)とするとき、線分\(AB\)の長さを共通接線の長さとよびます。共通接線の長さは外接線・内接線のいずれも、円の中心から接点に引いた線分が接線に垂直であることと三平方の定理を利用して求めることができます。

2円の半径を\(r,r’\)、中心間距離を\(d\)とすると

(共通外接線の長さ)

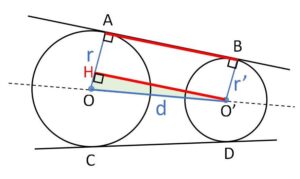
\(O’\)から\(OA\)に垂線\(O’H\)を引くと、四角形\(ABO’H\)は長方形になるので
\(AB=HO’\) (共通接線の長さ)
よって直角三角形\(OHO’\)について三平方の定理より
\(AB=HO’\)
\(=\sqrt{d^2-(r-r’)^2}\)
(\(r,r’\)の大小によらず成り立つ。またもう1つの外接線の長さ\(CD\)も同じ長さになる)

(共通内接線の長さ)

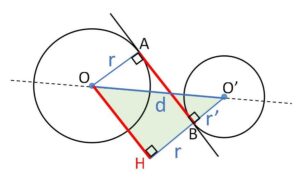
\(O\)から\(O’B\)の延長上に垂線\(OH\)を下ろすと、四角形\(OABH\)は長方形になるので
\(AB=OH\) (共通接線の長さ)
よって直角三角形\(OHO’\)で三平方の定理より
\(AB=OH\)
\(=\sqrt{d^2-(r+r’)^2}\)

(図には無いがもう1つの共通内接線の長さも同じ。なお2円が外接している場合 \(d=r+r’\) では2接点\(A,B\)は一致しますが、これを接線の長さ\(0\)とすれば上式に含めることができます)

 

 

・外接する2円と共通接線
2円が外接している場合の接線の性質について考えてみます。

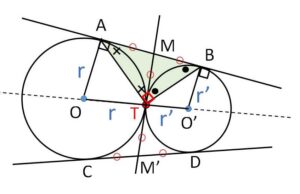
2円の接点を\(T\)、共通外接線と共通内接線の交点を\(M(M’)\)とすると
\(MA=MT\)、\(MT=MB\) だから
\(MA=MT=MB\)
よって直径を\(AB\)とする円の中心は\(M\)であり、この円は\(T\)を通るから
\(\angle ATB=90°\)
もう一方の共通外接線についても同様に
\(M’C=M’T=M’D\) であり \(AB=CD\) だから
\(AB=MM’=CD\)
となる。よって\(MM’\)は共通外接線の長さと等しくなる。(注)

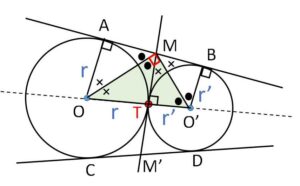
また図の\(△OMO’\)についても
2(●+x)=180°
より、\(\angle OMO’=90°\) となる。また\(MT\)を1辺とする2つの三角形の相似より
\(\displaystyle\frac{MT}{r}=\displaystyle\frac{r’}{MT}\)
よって \(MT=\sqrt{rr’}\) となるから、共通外接線の長さを
\(AB=2\sqrt{rr’}\)
と導くことができる。もちろん \(d=r+r’\) より
\(AB=\sqrt{d^2-(r-r’)^2}\)
\(=\sqrt{(r+r’)^2-(r-r’)^2}\)
\(=2\sqrt{rr’}\)
と導くともできる。

 

(注)について
2円が外部にある(離れている)場合にも
\(AB=MM’=CD\)
は成り立ちます。

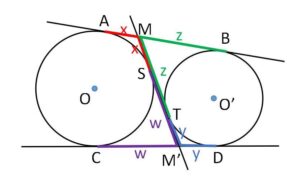
\(AB=CD=k\) (共通外接線の長さ) とおくと

\(x+z=k\)・・・①
\(y+w=k\)・・・②
\(x+w=MM’\)・・・③
\(y+z=MM’\)・・・④

①+② と ③+④より
\(x+y+z+w=2k\)
\(x+y+z+w=2MM’\)
となるので
\(MM’=k=AB=CD\)

ここで ①－③ と ②－③ より
\(z=w\)、\(x=y\)
であり、これらと③より④を導くことができるので、①②③④は実質①②③の3式であり未知数が4つなのでもう1つ式が必要になる。そこで共通内接線\(ST\)が
\(z-x=ST\)・・・⑤
と表されることと、共通外接線\(AB\)についての式
\(x+z=AB\)・・・①
より\(x,z\)を求めることができ、\(y,w\)も分かるので、4つの線分の長さを求めることができます。

 

 

(例題)
図の直線\(AB,CD\)は2円の共通接線である。円\(O_1,O_2\)の半径はそれぞれ\(3,2\)で、2円の中心間距離は\(5\sqrt{2}\)である。

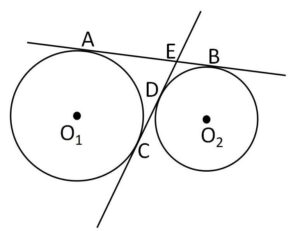
(1)共通外接線\(AB\)の長さと、共通内接線\(CD\)の長さを求めよ。
(2)\(DE,AE\)の長さをそれぞれ求めよ。

 

(解答)
(1)

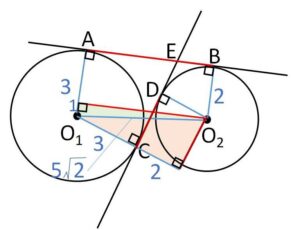
図より
\(AB=\sqrt{(5\sqrt{2})^2-(3-2)^2}\)
\(=\sqrt{49}\)
\(=7\)

\(CD=\sqrt{(5\sqrt{2})^2-(3+2)^2}\)
\(=\sqrt{25}\)
\(=5\)

(2)

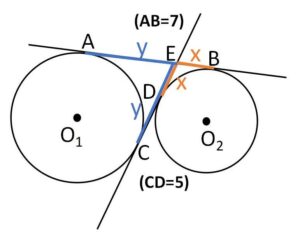
\(DE=x\)、\(AE=y\) とおくと図より
\(y+x=7\)・・・①
\(y-x=5\)・・・②

①②より
\(x=DE=1\)、\(y=AE=6\)

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接する複数の円　back→2円の位置関係